Semjonov Vlad, Ivasiro Alexander, 9. luokan oppilaat

Työ ja esitys graafisten ongelmien ratkaisemiseen. Tehtiin elektroninen peli ja esite graafisilla tehtävillä

Ladata:

Esikatselu:

Jos haluat käyttää esityksen esikatselua, luo Google-tili ja kirjaudu sisään siihen: https://accounts.google.com

Dian kuvatekstit:

opinnäytetyö Ongelmanratkaisu on yksi keino ymmärtää luonnonlakien välistä yhteyttä. Ongelmien ratkaiseminen on yksi tärkeimmistä tiedon toistamisen, lujittamisen ja itsetestauksen keinoista. Ratkaisemme useimmat fysikaaliset ongelmat analyyttisesti, mutta fysiikassa on ongelmia, jotka vaativat graafisen ratkaisun tai joissa esitetään graafi. Nämä tehtävät edellyttävät kykyä lukea ja analysoida kaaviota.

Aiheen relevanssi. 1) Graafisten ongelmien ratkaisemisen ja analysoinnin avulla voit ymmärtää ja muistaa fysiikan peruslait ja kaavat. 2) Fysiikan ja matematiikan yhtenäisen valtiontutkinnon KIM-malleihin sisältyy graafista sisältöä sisältäviä tehtäviä

Projektin tavoite: 1. Julkaista graafisten ongelmien ratkaisun itseopiskeluopas. 2. Luo sähköinen peli. Tehtävät: 1. Valitse graafisia tehtäviä eri aiheista. 2. Selvitä yleinen kuvio graafisten tehtävien ratkaisemisessa.

Graafin lukeminen Lämpöprosessien määritys Jakson, amplitudin, ... määrittäminen Ek, Er

Fysiikan 7-9 aikana voidaan korostaa lakeja, jotka ilmaistaan ​​suoralla riippuvuudella: X(t), m (ρ), I (q), F control(Δ x), F tr(N), F ( m), P (v) , p (F) p (h) , F а(V t) …, neliöllinen riippuvuus: E к =mv 2 /2 E р =CU 2 /2 E р =kx 2 /2

1 . Vertaa kondensaattoreiden kapasitanssia 2. Mikä kappaleen liikemäärän riippuvuuden massasta kaaviossa alla olevista pisteistä vastaa miniminopeutta? Pohditaanpa ongelmia 3 1 2

1. Mikä on jäykkyyskertoimien välinen suhde? 2. Alkuhetkellä levossa oleva kappale liikkuu vakiovoiman vaikutuksesta kuvan osoittamalla tavalla. Määritä tämän voiman projektion suuruus, jos kehon massa on 3 kg.

Huomaa, että P(V) on annettu ja kysymys koskee Ek 1:tä. Missä seuraavista suhteista ovat kolmen eri massaisen kappaleen kineettiset energiat ajankohtana, jolloin niiden nopeudet ovat samat? 2. Määritä 2 kg painavan kappaleen siirtymän ja ajan suhde projektion perusteella kappaleen liikemäärä hetkellä 2 s. (Alkunopeus on nolla.)

1 . Mikä seuraavista kuvaajista edustaa tarkimmin ennustetun nopeuden ja ajan välistä suhdetta? (Alkunopeus on nolla.) E Riippuvuudesta toiseen Graafista kuvaajaan

2. 1 kg painava kappale muuttaa nopeusprojektiotaan kuvan osoittamalla tavalla. Mikä seuraavista voimaprojisoinnista ajan funktiona kuvaajista vastaa tätä liikettä?

Fysiikan kurssilla on ongelmia useilla ratkaisutavoilla: 1. Laske keskinopeus 2. Määritä kappaleiden liikkeen projektioiden välinen suhde sillä hetkellä, kun kappaleiden nopeudet ovat samat. 10 5 0 V,x ; m/s t,s I II III

Menetelmä nro 1 10 5 0 V,x ; m/s t,c I II III a x= V 2x – V 1x t 2 – t 1 2 S=v 0 t+ at 2 /2

menetelmä nro 2 10 5 0 Vx; m/s t,s I II III Sx= (V 0 x + Vx) t/ 2

Menetelmä nro 3 10 5 0 V,x ; m/s t,s I II III S 3 x= 1 *S S 2 x= 2 *S S 1 x: S 2 x: S 3 x= 3: 2: 1 S 1 x= 3 *S

Extra slide Kolmas ratkaisumenetelmä ei luonnollisesti vaadi välilaskutoimituksia, joten se on nopeampi ja siten kätevämpi. Selvitetään, missä tehtävissä tällainen tilankäyttö on mahdollista.

Ratkaistujen ongelmien analyysi osoittaa, että jos X:n ja Y:n tulo on fysikaalinen suure, niin se on yhtä suuri kuin kaavion rajoittaman kuvan pinta-ala. P=IU, A=Fs S=vt, V=at, v0 =0 Δp/t=F, q=It Fa=V ρg,…. X Y

1. Kuvassa on kaavio tietyn kappaleen nopeuden projektiosta ajan funktiona. Määritä tämän kappaleen siirtymän projektio ja reitti 5 s liikkeen alkamisen jälkeen. Vx ; m/s 30-23 t; s 5 A) 5 m, 13 m B) 13 m, 5 m C) -1 m, 0 m D) 9 m, -4 m E) 15 m, 5 m

0 4 6 8 1 2 3 4 5 6 t, s V, m/s 2. Määritä pyöräilijän keskinopeus ajalla t=6s. Koko matkan koko ajan S x = S puolisuunnikkaan 4,7 m/s

Kehon liikemäärän muutoksen määrää kuvion pinta-ala - suorakulmio, jos voima on vakio, ja suorakulmainen kolmio, jos voima riippuu lineaarisesti ajasta. F t F t t F

3. Suurin kappaleen liikemäärän muutos 2s:ssa F t 1 .A 2 .B 3 .C 1 C B A Vihje: Ft=S f =  p

4. Määritä tähän kappaleeseen vaikuttava resultanttivoima käyttämällä kehon liikemäärän riippuvuutta ajasta. A) 3H B) 8H C) 12H D) 2H E) 16 trap P; kg* m/s 6 2 0 2 t ; c F = A p/t = (6-2)/2 = 2

Mekaaninen työ Mekaaninen työ, voiman suuruus ja suunta vakio, on numeerisesti yhtä suuri kuin suorakulmion pinta-ala. Voiman mekaaninen työ, jonka suuruus riippuu lineaarisen lain mukaisesta siirtymämoduulista, on numeerisesti yhtä suuri kuin suorakulmaisen kolmion pinta-ala. S 0 F F * s = A = S suorakaiteen muotoinen S 0 F A = ​​S suorakaiteen muotoinen

5. Kuvassa näkyy kehoon vaikuttavan voiman riippuvuus siirtymästä. Määritä tämän voiman tekemä työ, kun keho liikkuu 20 cm. A) 20 J. B) 8J. C) 0,8 J. D) 40 J. E) 0,4 J. trap cm metreihin

Laske varaus 4 I,A 6 2 U,B 4 8 12 16 20 24 Laske vastus. Laske A, Δ Ek 4 s. Laske jousen Er

6. Muuttuvan voiman vaikutuksesta kappale, jonka massa on 1 kg, muuttaa nopeusprojektioaan ajan kuluessa kuvan osoittamalla tavalla. Tämän voiman resultantin työtä on vaikea määrittää 8 sekunnissa liikkeen alkamisesta A) 512J B) 128J C) 112J D) 64J E) 132J A=FS , S= S (t=4c) =32m , F =ma, a =(v -v0)t = 2 m/s 2

Johtopäätös Työmme tuloksena julkaisimme esitteen graafisista tehtävistä itsenäiseen ratkaisuun ja loimme elektronisen pelin. Työ osoittautui hyödylliseksi yhtenäistettyyn valtionkokeeseen valmistautumiseen sekä fysiikasta kiinnostuneille opiskelijoille. Jatkossa muun tyyppisten ongelmien pohtiminen ja niiden ratkaisu.

Fysikaalisten suureiden toiminnalliset riippuvuudet. Yleiset menetelmät, tekniikat ja lähestymistavan säännöt graafisten ongelmien ratkaisemiseen -projekti "TALKING LINE" MBOU Lukio nro 8 Yuzhno-Sakhalinsk Suorittanut: Semjonov Vladislav, Ivasiro Alexander, 9. luokan "A" oppilaat

Tietolähteet. 1. Lukashik V.I., Ivanova E.V. Fysiikan ongelmien kokoelma. Moskova “Enlightenment” 2000 2. Stepanova G.I Fysiikan tehtäväkokoelma M. Enlightenment 1995 3. Rymkevich A.P. Kokoelma fysiikan ongelmia Moskova. Koulutus 1988. 4. www.afportal.ru 5. A.V. Peryshkin, E.M. Gutnik Fysiikan oppikirja luokille 7, 8, 9. 6. GIA-materiaalit 7. S.E. Kamenetsky, V.P. Orekhov Menetelmät fysiikan ongelmien ratkaisemiseen lukiossa. M: Koulutus, 1987. 8. V.A. Balazs Fysiikan tehtäviä ja niiden ratkaisumenetelmiä. Moskovan "valistus" 1983

Asiantuntijat todistavat teknisen koulutuksen edun humanistisiin tieteisiin nähden, he osoittavat, että Venäjä tarvitsee kipeästi korkeasti koulutettuja insinöörejä ja teknisiä asiantuntijoita, ja tämä suuntaus jatkuu paitsi vuonna 2014, myös tulevina vuosina. Henkilöstönvalintaasiantuntijoiden mukaan jos maa odottaa talouskasvua lähivuosina (ja sille on edellytykset), niin on erittäin todennäköistä, että Venäjän koulutuspohja ei tule toimeen monilla sektoreilla (korkea teknologia, teollisuus) . "Tällä hetkellä työmarkkinoilla on akuutti pula insinööri- ja teknisten erikoisalojen asiantuntijoista, IT-alalta: ohjelmoijia, ohjelmistokehittäjiä. Lähes kaikkien erikoisalojen insinöörejä on edelleen kysyntää. Samalla markkinat ovat ylikylläiset lakimiehistä, taloustieteilijöistä, toimittajista, psykologeista”, sanoo Unique Specialists -rekrytointitoimiston pääjohtaja Ekaterina Krupina. Pitkän aikavälin ennusteita vuoteen 2020 asti tekevät analyytikot luottavat teknisten erikoisalojen kysynnän kasvavan nopeasti joka vuosi. Ongelman relevanssi. Siksi fysiikan yhtenäiseen valtionkokeeseen valmistautumisen laatu on tärkeää. Fyysisten ongelmien ratkaisumenetelmien hallinta on ratkaisevan tärkeää. Useat fyysiset tehtävät ovat graafisia tehtäviä. 1) Graafisten ongelmien ratkaisemisen ja analysoinnin avulla voit ymmärtää ja muistaa fysiikan peruslait ja kaavat. 2) Yhdistetyn fysiikan valtiontutkinnon KIM-malleissa on graafista sisältöä sisältäviä tehtäviä.

Lataa työ esityksen kanssa.

PROJEKTITYÖN TAVOITE:

Graafisten ongelmien tyyppien, lajikkeiden, ominaisuuksien ja ratkaisumenetelmien tutkiminen .

TYÖN TAVOITTEET:

1. Graafisten tehtävien kirjallisuuden opiskelu; 2. Unified State Exam -materiaalien tutkiminen (graafisten tehtävien yleisyys ja monimutkaisuus); 3. Yleisten ja erityisten graafisten ongelmien tutkiminen fysiikan eri aloilta, monimutkaisuusaste. 4. Ratkaisumenetelmien tutkiminen; 5. Sosiologisen tutkimuksen tekeminen koululaisten ja opettajien keskuudessa.

Fysiikan ongelma

Metodologisessa ja opetuskirjallisuudessa opettavaiset fyysiset tehtävät ymmärretään asianmukaisesti valittuina harjoituksina, joiden päätarkoituksena on tutkia fyysisiä ilmiöitä, muodostaa käsitteitä, kehittää opiskelijoiden fyysistä ajattelua ja juurruttaa heihin kykyä soveltaa tietojaan käytännössä.

Opiskelijoiden opettaminen fyysisten ongelmien ratkaisemiseen on yksi vaikeimmista pedagogisista ongelmista. Mielestäni tämä ongelma on erittäin ajankohtainen. Projektini tavoitteena on ratkaista kaksi ongelmaa:

1. Auttaa opettamaan koululaisille kykyä ratkaista graafisia ongelmia;

2. Ota opiskelijat mukaan tämäntyyppiseen työhön.

Ongelman ratkaiseminen ja analysointi antaa sinun ymmärtää ja muistaa fysiikan peruslait ja kaavat, luoda käsityksen niiden ominaispiirteistä ja sovellusrajoista. Ongelmat kehittävät taitoja käyttää aineellisen maailman yleisiä lakeja ratkaisemaan käytännön ja kasvatuksellisesti tärkeitä asioita. Ongelmanratkaisukyky on paras kriteeri arvioitaessa ohjelmamateriaalin opiskelun syvyyttä ja sen assimilaatiota.

Tutkimuksissa, joissa selvitettiin, missä määrin opiskelijat ovat hallitseneet ongelmanratkaisukykyyn sisältyviä yksittäisiä operaatioita, on havaittu, että 30-50 % eri luokkien opiskelijoista ilmoittaa, että heiltä puuttuu tällaisia ​​taitoja.

Kyvyttömyys ratkaista ongelmia on yksi tärkeimmistä syistä fysiikan opiskelun onnistumisen heikkenemiseen. Tutkimukset ovat osoittaneet, että kyvyttömyys ratkaista ongelmia itsenäisesti on tärkein syy kotitehtävien epäsäännölliseen suorittamiseen. Vain pieni osa opiskelijoista hallitsee ongelmien ratkaisukyvyn, jota he pitävät yhtenä tärkeimmistä edellytyksistä fysiikan tiedon laadun parantamiselle.

Tämä oppimiskäytännön tila voidaan selittää selkeiden vaatimusten puutteella tämän taidon muodostumiselle, sisäisten motivaatioiden ja opiskelijoiden kognitiivisen kiinnostuksen puutteella.

Ongelmien ratkaisemisessa fysiikan opetusprosessissa on monitahoisia toimintoja:

• Teoreettisen tiedon hallinta.
• Fysikaalisten ilmiöiden ja suureiden käsitteiden hallinta.
• Opiskelijoiden henkinen kehitys, luova ajattelu ja erityiskyvyt.
• Esittelee opiskelijat tieteen ja tekniikan saavutuksiin.
• Kehittää kovaa työtä, sinnikkyyttä, tahtoa, luonnetta ja päättäväisyyttä.
• Se on keino seurata opiskelijoiden tietoja, taitoja ja kykyjä.

Graafinen tehtävä.

Graafiset tehtävät ovat ratkaisuprosessissa olevia tehtäviä, joita käytetään kaavioita, kaavioita, taulukoita, piirustuksia ja kaavioita.

Esimerkiksi:

1. Muodosta kaavio tasaisen liikkeen reitistä, jos v = 2 m/s tai tasaisesti kiihtyvästä liikkeestä, jos v 0 = 5 m/s ja a = 3 m/s 2 .

2. Mitä ilmiöitä graafin kukin osa kuvaa...

3. Kumpi keho liikkuu nopeammin

4. Millä alueella keho liikkui nopeammin?

5. Määritä kuljettu matka nopeuskäyrästä.

6. Missä liikkeen osassa keho oli levossa. Nopeus kasvoi ja laski.

Graafisten tehtävien ratkaiseminen auttaa ymmärtämään fysikaalisten suureiden toiminnallista suhdetta, kehittämään graafisen käytön taitoja ja kykyä työskennellä asteikkojen kanssa.

Graafeiden roolin perusteella tehtävien ratkaisussa ne voidaan jakaa kahteen tyyppiin: - tehtävät, joiden kysymykseen vastaus löytyy graafin rakentamisen tuloksena; - tehtävät, joihin vastaus löytyy kaaviota analysoimalla.

Graafisia tehtäviä voidaan yhdistää kokeellisiin tehtäviin.

Esimerkiksi:

Määritä puupalkan paino vedellä täytetyllä dekantterilasilla...

Valmistautuminen graafisten tehtävien ratkaisemiseen.

Graafisten tehtävien ratkaisemiseksi opiskelijan tulee tuntea erilaisia ​​funktionaalisia riippuvuuksia, mikä tarkoittaa graafien ja akselien ja graafien leikkausta keskenään. Sinun on ymmärrettävä, miten riippuvuudet eroavat, esim. x = x 0 + vt ja x = v 0 t + kohdassa 2 /2 tai x = x m sinω 0 t ja x = - x m sinω 0 t; x =x m sin(ω 0 t+ α) ja x =x m cos (ω 0 t+ α) jne.

Valmistelusuunnitelman tulee sisältää seuraavat osat:

· a) Toista funktioiden kuvaajat (lineaariset, neliölliset, potenssit) · b) Selvitä, mikä rooli graafilla on fysiikassa, mitä tietoa ne kuljettavat. · c) Systematisoi fyysisiä ongelmia niissä olevien kuvaajien merkityksen mukaan. · d) Tutkimusmenetelmiä ja tekniikoita fysikaalisten graafien analysointiin · e) Kehittää algoritmi graafisten ongelmien ratkaisemiseksi fysiikan eri aloilla · f) Selvitä graafisten tehtävien ratkaisun yleinen malli. Ongelmanratkaisumenetelmien hallitsemiseksi on tarpeen ratkaista suuri määrä erilaisia ​​​​ongelmia noudattaen periaatetta - "Yksinkertaisesta monimutkaiseen". Aloittaen yksinkertaisista, hallitse ratkaisumenetelmiä, vertaile, yleistä erilaisia ​​ongelmia sekä kaavioiden perusteella että taulukoiden, kaavioiden, kaavioiden avulla. Sinun tulee kiinnittää huomiota suureiden merkitsemiseen koordinaattiakseleilla (fysikaalisten suureiden yksiköt, useiden tai useiden etuliitteiden läsnäolo), mittakaavaan, toiminnallisen riippuvuuden tyyppiin (lineaarinen, neliöllinen, logaritminen, trigonometrinen jne.), kaavioiden kaltevuuskulmat, kaavioiden leikkauspisteet koordinaattiakseleiden kanssa tai kuvaajat keskenään. Erityisen varovaisesti on lähestyttävä ongelmia, jotka liittyvät luontaisiin "virheisiin", samoin kuin ongelmia mittauslaitteiden vaakojen valokuvien kanssa. Tässä tapauksessa on tarpeen määrittää oikein mittauslaitteiden jakoarvo ja lukea tarkasti mitattujen määrien arvot. Geometriseen optiikkaan liittyvissä ongelmissa on erityisen tärkeää rakentaa huolellisesti ja tarkasti säteet ja määrittää niiden leikkauspisteet akselien ja toistensa kanssa.

Kuinka ratkaista grafiikkaongelmat

Fyysisten ongelmien ratkaisun yleisen algoritmin hallinta

1. Ongelmaolosuhteiden analyysin suorittaminen tunnistamalla ongelmassa kuvatut järjestelmätehtävät, ilmiöt ja prosessit sekä määrittämällä niiden esiintymisen ehdot

2. Ongelmatilanteiden ja ratkaisuprosessin koodaaminen eri tasoilla:

a) lyhyt kuvaus ongelmatilanteista;

b) piirustusten ja sähkökaavioiden tekeminen;

c) piirustusten, kaavioiden, vektorikaavioiden toteuttaminen;

d) yhtälön (yhtälöjärjestelmän) kirjoittaminen tai loogisen päätelmän laatiminen

3. Sopivan menetelmän ja menetelmien tunnistaminen tietyn ongelman ratkaisemiseksi

4. Yleisen algoritmin soveltaminen erityyppisten ongelmien ratkaisemiseen

Ongelman ratkaiseminen alkaa ehtojen lukemisesta. Sinun on varmistettava, että kaikki ehdon termit ja käsitteet ovat opiskelijoille selviä. Epäselvät termit selvennetään ensimmäisen lukemisen jälkeen. Samalla on korostettava, mitä ilmiötä, prosessia tai kappaleiden ominaisuutta ongelmassa kuvataan. Sitten ongelma luetaan uudelleen, mutta tiedot ja vaaditut määrät on korostettu. Ja vasta tämän jälkeen suoritetaan lyhyt tallennus ongelman olosuhteista.

Suunnittelu

Suuntautumistoiminto mahdollistaa tehtävän havaittujen ehtojen toissijaisen analyysin, jonka tuloksena tunnistetaan fysikaaliset teoriat, lait, yhtälöt, jotka selittävät tiettyä tehtävää. Sitten tunnistetaan menetelmät yhden luokan ongelmien ratkaisemiseksi ja löydetään optimaalinen menetelmä tämän ongelman ratkaisemiseksi. Opiskelijatoiminnan tuloksena syntyy ratkaisusuunnitelma, joka sisältää ketjun loogisia toimia. Toimenpiteiden oikeellisuutta ongelman ratkaisusuunnitelman laatimiseksi valvotaan.

Ratkaisuprosessi

Ensinnäkin on tarpeen selventää jo tunnettujen toimien sisältöä. Orientointitoiminta tässä vaiheessa sisältää jälleen kerran ongelman ratkaisumenetelmän korostamisen ja ratkaistavan ongelman tyypin selvittämisen ehtojen asettamismenetelmällä. Seuraava askel on suunnittelu. Ongelman ratkaisemiseksi suunnitellaan menetelmä, laitteisto (looginen, matemaattinen, kokeellinen), jonka avulla on mahdollista suorittaa sen jatkoratkaisu.

Ratkaisuanalyysi

Ongelmanratkaisuprosessin viimeinen vaihe on saadun tuloksen tarkistaminen. Se suoritetaan uudelleen samoilla toimilla, mutta toimien sisältö muuttuu. Suuntautumistoiminto on sen olemuksen selvittäminen, mikä on tarkistettava. Ratkaisun tuloksia voivat olla esimerkiksi kertoimien arvot, mekanismien ja koneiden fysikaaliset vakioominaisuudet, ilmiöt ja prosessit.

Ongelman ratkaisemisesta saadun tuloksen tulee olla uskottava ja terveen järjen mukainen.

Graafisten tehtävien yleisyys tietokonesimulaatiokoneissa Unified State Examination -tehtävissä

Useita vuosia (2004 - 2013) suoritettu Unified State Exam -materiaalien tutkiminen osoitti, että fysiikan eri osien graafiset ongelmat ovat yleisiä Unified State Exam -tehtävissä fysiikan eri osa-alueilla. Tehtävissä A: mekaniikassa - 2-3 molekyylifysiikassa - 1 termodynamiikassa - 3 sähködynamiikassa - 3-4 optiikassa - 1-2 kvanttifysiikassa - 1 atomi- ja ydinfysiikassa - 1 tehtävissä B: mekaniikassa - 1 molekyylifysiikassa - 1 termodynamiikassa - 1 sähködynamiikassa - 1 optiikassa - 1 kvanttifysiikassa - 1 atomi- ja ydinfysiikassa - 1 tehtävissä C: mekaniikassa - molekyylifysiikassa - termodynamiikassa - 1 sähködynamiikassa - 1 in optiikka - 1 kvanttifysiikassa - atomi- ja ydinfysiikassa - 1

Meidän tutkimuksemme

A. Virheiden analysointi graafisten ongelmien ratkaisussa

Graafisten ongelmien ratkaisemisen analyysi osoitti, että esiintyy seuraavia yleisiä virheitä:

Virheet kaavioiden lukemisessa;

Virheet operaatioissa vektorisuureiden kanssa;

Virheet isoprosessikaavioita analysoitaessa;

Virheet sähkösuureiden graafisessa riippuvuudessa;

Virheet rakennettaessa geometrisen optiikan lakeja;

Virheet graafisissa tehtävissä kvanttilakeista ja valosähköisestä vaikutuksesta;

Virheitä atomifysiikan lakien soveltamisessa.

B. Sosiologinen tutkimus

Selvittääksemme, kuinka koululaiset ovat tietoisia graafisista tehtävistä, teimme sosiologisen tutkimuksen.

Esitimme koulumme oppilaille ja opettajille seuraavat kysymykset: profiilit:

1. 1. Mikä on grafiikkatehtävä?

a) ongelmia kuvien kanssa;

b) kaavioita sisältävät tehtävät, kaaviot;

c) En tiedä.

1. 2. Mitä varten graafiset tehtävät ovat?

b) kehittää kykyä rakentaa kuvaajia;

c) En tiedä.

3. Pystytkö ratkaisemaan graafisia ongelmia?

a) kyllä; b) ei; c) en ole varma ;

4. Haluatko oppia ratkaisemaan graafisia ongelmia?

A) kyllä ; b) ei; c) Minun on vaikea vastata.

50 henkilöä haastateltiin. Kyselyn tuloksena saatiin seuraavat tiedot:

JOHTOPÄÄTÖKSET:

1. "Graafiset tehtävät" -projektin parissa työskentelyn tuloksena tutkimme graafisten tehtävien ominaisuuksia.
2. Tutkimme graafisten ongelmien ratkaisumetodologian ominaisuuksia.
3. Analysoimme tyypillisiä virheitä.
4. Teki sosiologisen tutkimuksen.

Toiminnan heijastus:

1. Meille oli mielenkiintoista työskennellä graafisten tehtävien ongelman parissa.
2. Opimme tekemään tutkimustoimintaa, vertailemaan ja vertailemaan tutkimustuloksia.
3. Huomasimme, että graafisten ongelmien ratkaisumenetelmien hallinta on välttämätöntä fysikaalisten ilmiöiden ymmärtämiseksi.
4. Huomasimme, että graafisten ongelmien ratkaisumenetelmien hallinta on välttämätöntä Unified State Extensin menestyksekkääksi läpäisemiseksi.

Jos lineaarisessa ohjelmointitehtävässä on vain kaksi muuttujaa, se voidaan ratkaista graafisesti.

Harkitse lineaarista ohjelmointiongelmaa kahdella muuttujalla ja :
(1.1) ;
(1.2)
Tässä on mielivaltaisia ​​numeroita. Tehtävänä voi olla joko löytää maksimi (max) tai löytää minimi (min). Rajoitusjärjestelmä voi sisältää sekä kylttejä että kylttejä.

Toteutettavien ratkaisujen alueen rakentaminen

Graafinen menetelmä tehtävän (1) ratkaisemiseksi on seuraava.
Ensin piirrämme koordinaattiakselit ja valitsemme mittakaavan. Kukin rajoitusjärjestelmän (1.2) epäyhtälö määrittelee puolitason, jota rajoittaa vastaava suora.

Eli ensimmäinen eriarvoisuus
(1.2.1)
määrittelee puolitason, jota rajoittaa suora viiva. Toisella puolella tätä suoraa ja toisella puolella. Hyvin suoralla linjalla. Selvittääksemme, kummalla puolella epäyhtälö (1.2.1) pätee, valitsemme mielivaltaisen pisteen, joka ei ole suoralla. Seuraavaksi korvataan tämän pisteen koordinaatit (1.2.1). Jos epäyhtälö pätee, puolitaso sisältää valitun pisteen. Jos epäyhtälö ei päde, puolitaso sijaitsee toisella puolella (ei sisällä valittua pistettä). Varjostaa puolitaso, jolle epäyhtälö (1.2.1) pätee.

Teemme saman järjestelmän (1.2) jäljellä oleville epäyhtälöille. Näin saamme varjostettuja puolitasoja. Toteutettavien ratkaisujen alueen pisteet täyttävät kaikki epäyhtälöt (1.2). Siksi graafisesti toteutettavien ratkaisujen alue (ADA) on kaikkien rakennettujen puolitasojen leikkauspiste. ODR:n varjostus. Se on kupera monikulmio, jonka pinnat kuuluvat rakennettuihin suoriin. ODF voi olla myös rajoittamaton kupera kuvio, segmentti, säde tai suora viiva.

Saattaa myös esiintyä, että puolitasot eivät sisällä yhteisiä pisteitä. Tällöin toteutettavissa olevien ratkaisujen alue on tyhjä joukko. Tähän ongelmaan ei ole ratkaisuja.

Menetelmää voidaan yksinkertaistaa. Sinun ei tarvitse varjostaa jokaista puolitasoa, vaan rakentaa ensin kaikki suorat viivat
(2)
Valitse seuraavaksi mielivaltainen piste, joka ei kuulu mihinkään näistä viivoista. Korvaa tämän pisteen koordinaatit epäyhtälöjärjestelmässä (1.2). Jos kaikki epäyhtälöt täyttyvät, toteutettavien ratkaisujen alue on rajattu rakennetuilla suorilla ja se sisältää valitun pisteen. Varjostamme toteutettavissa olevien ratkaisujen alueen viivojen rajoja pitkin siten, että se sisältää valitun pisteen.

Jos ainakin yksi epäyhtälö ei täyty, valitse toinen piste. Ja niin edelleen, kunnes löydetään yksi piste, jonka koordinaatit täyttävät järjestelmän (1.2).

Tavoitefunktion ääripään löytäminen

Meillä on siis varjostettu alue toteutettavissa olevista ratkaisuista (ADA). Sitä rajoittaa katkoviiva, joka koostuu segmenteistä ja säteistä, jotka kuuluvat rakennettuihin suoriin (2). ODS on aina kupera joukko. Se voi olla joko rajoitettu joukko tai ei ole rajoitettu joidenkin suuntien mukaan.

Nyt voimme etsiä tavoitefunktion ääripäätä
(1.1) .

Voit tehdä tämän valitsemalla minkä tahansa numeron ja rakentamalla suoran
(3) .
Esittelyn helpottamiseksi oletamme, että tämä suora kulkee ODR:n läpi. Tällä rivillä tavoitefunktio on vakio ja yhtä suuri kuin . tällaista suoraa kutsutaan funktiotasoviivaksi. Tämä suora jakaa tason kahteen puolitasoon. Yhdellä puolitasolla
.
Toisessa puolitasossa
.
Toisin sanoen suoran (3) toisella puolella tavoitefunktio kasvaa. Ja mitä pidemmälle siirrämme pistettä suoralta (3), sitä suurempi arvo on. Suoran (3) toisella puolella tavoitefunktio pienenee. Ja mitä pidemmälle siirrämme pistettä suoralta (3) toiselle puolelle, sitä pienempi arvo on. Jos piirretään suoran (3) suuntainen suora, niin uusi suora on myös tavoitefunktion tasoviiva, mutta jolla on eri arvo.

Siten tavoitefunktion maksimiarvon löytämiseksi on vedettävä suoran (3) suuntainen suora, mahdollisimman kauas siitä arvojen nousun suuntaan ja joka kulkee vähintään yhden pisteen kautta. ODD:sta. Tavoitefunktion minimiarvon löytämiseksi on vedettävä suoran (3) suuntainen suora viiva siitä mahdollisimman kauas laskevien arvojen suuntaan ja joka kulkee vähintään yhden ODD:n pisteen läpi.

Jos ODR on rajoittamaton, voi syntyä tapaus, jossa tällaista suoraa linjaa ei voida vetää. Eli riippumatta siitä, kuinka poistamme suoran tasoviivasta (3) nousun (laskemisen) suuntaan, suora kulkee aina ODR:n läpi. Tässä tapauksessa se voi olla mielivaltaisen suuri (pieni). Siksi ei ole olemassa enimmäisarvoa (minimiarvoa). Ongelmaan ei ole ratkaisuja.

Tarkastellaan tilannetta, jossa ääriviiva, joka on yhdensuuntainen muotoa (3) olevan mielivaltaisen suoran kanssa, kulkee ODR-polygonin yhden kärjen kautta. Kaaviosta määritetään tämän kärjen koordinaatit. Sitten tavoitefunktion enimmäisarvo (minimi) määritetään kaavalla:
.
Ratkaisu ongelmaan on
.

Saattaa myös olla tapaus, jossa suora on yhdensuuntainen ODR:n toisen pinnan kanssa. Sitten suora kulkee ODR-polygonin kahden kärjen läpi. Määritämme näiden kärkien koordinaatit. Voit määrittää tavoitefunktion enimmäisarvon (minimiarvon) käyttämällä minkä tahansa näiden kärkien koordinaatteja:
.
Ongelmaan on äärettömän monta ratkaisua. Ratkaisu on mikä tahansa piste, joka sijaitsee segmentillä pisteiden ja , mukaan lukien pisteet ja itsensä.

Esimerkki lineaarisen ohjelmointitehtävän ratkaisemisesta graafisella menetelmällä

Tehtävä

Yritys valmistaa kahden mallin A ja B mekkoja. Kangastyyppejä on kolme. Yhden mallin A mekon valmistamiseksi tarvitaan 2 m ensimmäisen tyypin kangasta, 1 m toisen tyypin kangasta ja 2 m kolmannen tyypin kangasta. Yhden mallin B mekon valmistamiseksi tarvitaan 3 m ensimmäisen tyypin kangasta, 1 m toisen tyypin kangasta ja 2 m kolmannen tyypin kangasta. Ensimmäisen tyypin kangasvarastot ovat 21 m, toisen tyypin - 10 m, kolmannen tyypin - 16 m. Yhden A-tyypin tuotteen julkaisu tuo 400 den tuloja. yksikköä, yksi tuotetyyppi B - 300 den. yksiköitä

Laadi tuotantosuunnitelma, joka tarjoaa yritykselle suurimmat tulot. Ratkaise ongelma graafisesti.

Ratkaisu

Olkoon muuttujat ja osoittavat valmistettujen mekkojen lukumäärää, mallit A ja B, vastaavasti. Sitten kulutetun ensimmäisen tyypin kankaan määrä on:
(m)
Toisen tyypin kankaan kulutettu määrä on:
(m)
Kolmannen tyypin kankaan kulutettu määrä on:
(m)
Koska valmistettujen mekkojen määrä ei voi olla negatiivinen, niin
Ja .
Tuotot valmistetuista mekoista ovat:
(den. yksikköä)

Sitten ongelman taloudellis-matemaattinen malli on seuraavanlainen:

Ratkaisemme sen graafisesti.
Piirrämme koordinaattiakselit ja .

Rakennamme suoraa linjaa.
klo .
klo .
Piirrä suora viiva pisteiden (0; 7) ja (10.5; 0) läpi.

Rakennamme suoraa linjaa.
klo .
klo .
Piirrä suora viiva pisteiden (0; 10) ja (10; 0) läpi.

Rakennamme suoraa linjaa.
klo .
klo .
Piirrä suora viiva pisteiden (0; 8) ja (8; 0) läpi.

Varjostamme alueen niin, että piste (2; 2) putoaa varjostettuun osaan. Saamme nelikulmion OABC.

(A1.1) .
klo .
klo .
Piirrä suora viiva pisteiden (0; 4) ja (3; 0) läpi.

Huomaamme lisäksi, että koska tavoitefunktion ja tavoitefunktion kertoimet ovat positiivisia (400 ja 300), se kasvaa ja kasvaa. Piirretään suoran (A1.1) kanssa yhdensuuntainen suora viiva mahdollisimman kauas siitä kasvun suuntaan ja joka kulkee vähintään yhden nelikulmion OABC pisteen läpi. Tällainen viiva kulkee pisteen C kautta. Konstruktiosta määritetään sen koordinaatit.
.

Ongelman ratkaisu: ;

Vastaus

.
Eli suurimman tulon saamiseksi on tehtävä 8 mallin A mekkoa. Tulot ovat 3200 deniä. yksiköitä

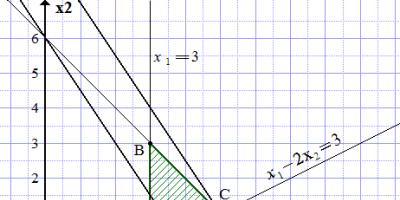
Esimerkki 2

Tehtävä

Ratkaise lineaarisen ohjelmoinnin tehtävä graafisesti.

Ratkaisu

Ratkaisemme sen graafisesti.
Piirrämme koordinaattiakselit ja .

Rakennamme suoraa linjaa.
klo .
klo .
Piirrä suora viiva pisteiden (0; 6) ja (6; 0) läpi.

Rakennamme suoraa linjaa.
Täältä.
klo .
klo .
Piirrä suora viiva pisteiden (3; 0) ja (7; 2) läpi.

Rakennamme suoraa linjaa.
Rakennamme suoran (abskissa-akselin).

Sallittujen ratkaisujen alue (ADA) on rajoitettu rakennetuilla suorilla viivoilla. Selvittääksemme kumman puolen huomaamme, että piste kuuluu ODR:ään, koska se täyttää epätasa-arvojärjestelmän:

Varjostamme alueen rakennettujen viivojen rajoilla niin, että piste (4; 1) putoaa varjostettuun osaan. Saamme kolmion ABC.

Rakennamme mielivaltaisen rivin tavoitefunktion tasolle, esim.
.
klo .
klo .
Piirrä suora tasoviiva pisteiden (0; 6) ja (4; 0) läpi.
Koska tavoitefunktio kasvaa kasvaessa ja , vedetään suora viiva, joka on yhdensuuntainen tasoviivan kanssa ja mahdollisimman kauas siitä lisääntymissuuntaan ja kulkee vähintään yhden kolmion ABC pisteen läpi. Tällainen viiva kulkee pisteen C kautta. Konstruktiosta määritetään sen koordinaatit.
.

Ongelman ratkaisu: ;

Vastaus

Esimerkki ratkaisun puuttumisesta

Tehtävä

Ratkaise lineaarisen ohjelmoinnin tehtävä graafisesti. Etsi tavoitefunktion suurin ja pienin arvo.

Ratkaisu

Ratkaisemme ongelman graafisesti.
Piirrämme koordinaattiakselit ja .

Rakennamme suoraa linjaa.
klo .
klo .
Piirrä suora viiva pisteiden (0; 8) ja (2,667; 0) läpi.

Rakennamme suoraa linjaa.
klo .
klo .
Piirrä suora viiva pisteiden (0; 3) ja (6; 0) läpi.

Rakennamme suoraa linjaa.
klo .
klo .
Piirrä suora viiva pisteiden (3; 0) ja (6; 3) läpi.

Suorat viivat ovat koordinaattiakseleita.

Sallittujen ratkaisujen alue (ADA) on rajoitettu rakennetuilla suorilla ja koordinaattiakseleilla. Selvittääksemme kumman puolen huomaamme, että piste kuuluu ODR:ään, koska se täyttää epätasa-arvojärjestelmän:

Varjostamme alueen niin, että piste (3; 3) putoaa varjostettuun osaan. Saamme rajattoman alueen, jota rajoittaa katkoviiva ABCDE.

Rakennamme mielivaltaisen rivin tavoitefunktion tasolle, esim.
(A3.1) .
klo .
klo .
Piirrä suora viiva pisteiden (0; 7) ja (7; 0) läpi.
Koska ja kertoimet ovat positiivisia, se kasvaa kasvaessa ja .

Maksimiarvon löytämiseksi sinun on piirrettävä yhdensuuntainen viiva, joka on mahdollisimman kaukana kasvusuunnassa ja kulkee vähintään yhden ABCDE-alueen pisteen läpi. Koska alue on kuitenkin rajaton suurten ja arvojen puolella, tällaista suoraa ei voida vetää. Riippumatta siitä, minkä viivan piirrämme, alueella on aina pisteitä, jotka ovat kauempana kasvavan ja . Siksi enimmäismäärää ei ole. voit tehdä siitä niin suuren kuin haluat.

Etsimme minimiä. Piirretään suoran (A3.1) kanssa yhdensuuntainen suora viiva siitä mahdollisimman kauas pienenemissuuntaan ja joka kulkee ainakin yhden ABCDE-alueen pisteen läpi. Tällainen viiva kulkee pisteen C kautta. Konstruktiosta määritetään sen koordinaatit.
.
Tavoitefunktion vähimmäisarvo:

Vastaus

Maksimiarvoa ei ole.
Minimiarvo
.

Usein fyysisen prosessin graafinen esitys tekee siitä visuaalisemman ja helpottaa siten tarkasteltavan ilmiön ymmärtämistä. Joskus kaavioita käytetään laajasti käytännössä erilaisten ongelmien ratkaisemiseen, mikä mahdollistaa laskelmien merkittävän yksinkertaistamisen. Kyky rakentaa ja lukea niitä on nykyään monille asiantuntijoille pakollinen.

Pidämme seuraavia tehtäviä graafisina tehtävinä:

• rakentamiseen, jossa piirustukset ja piirustukset ovat erittäin hyödyllisiä;
• kaavioita ratkaistaan ​​käyttämällä vektoreita, kaavioita, kaavioita, kaavioita ja nomogrammeja.

1) Pallo heitetään pystysuoraan ylöspäin maasta alkunopeudella v O. Piirrä kuvaaja pallon nopeudesta ajan funktiona olettaen, että maahan kohdistuvat iskut ovat täysin kimmoisia. Jätä ilmanvastus huomioimatta. [ratkaisu ]

2) Junasta myöhästynyt matkustaja huomasi, että toiseksi viimeinen auto ohitti hänet t 1 = 10 s, ja viimeinen - varten t 2 = 8 s. Olettaen, että junan liike on tasaisesti kiihtynyt, määritä viiveaika. [ratkaisu ]

3) Korkeassa huoneessa H kattoon on kiinnitetty toisessa päässä kevyt jäykkyysjousi k, jonka pituus on muotoutumattomassa tilassa l o (l o< H ). Lattialle jousen alle asetetaan korkeuslohko x pohja-alueen kanssa S, valmistettu materiaalista, jonka tiheys ρ . Muodosta kaavio lohkon paineesta lattiassa suhteessa lohkon korkeuteen. [ratkaisu ]

4) Vika ryömii akselia pitkin Härkä. Määritä sen keskimääräinen liikkeen nopeus koordinaattipisteiden välisellä alueella x 1 = 1,0 m Ja x 2 = 5,0 m, jos tiedetään, että hyönteisen nopeuden ja sen koordinaatin tulo pysyy vakiona koko ajan, c = 500 cm2/s. [ratkaisu ]

5) Massalohkoon 10 kg vaakasuoraan pintaan kohdistetaan voima. Ottaen huomioon, että kitkakerroin on yhtä suuri kuin 0,7 , määrittele:

• kitkavoima kotelolle, jos F = 50 N ja suunnattu vaakasuoraan.
• kitkavoima kotelolle, jos F = 80 N ja suunnattu vaakasuoraan.
• piirrä kaavio lohkon kiihtyvyydestä vaakasuuntaisen voiman funktiona.
• Mikä on vähimmäisvoima, joka tarvitaan köyden vetämiseen, jotta lohko liikkuu tasaisesti? [ratkaisu ]

6) Sekoittimeen on kytketty kaksi putkea. Jokaisessa putkessa on hana, jolla voidaan säätää veden virtausta putken läpi muuttamalla se nollasta maksimiarvoon J o = 1 l/s. Vesi virtaa putkissa lämpötiloissa t1 = 10 °C Ja t2 = 50 °C. Piirrä kaavio sekoittimesta ulos virtaavan veden maksimivirtauksesta veden lämpötilan funktiona. Älä huomioi lämpöhäviöitä. [ratkaisu ]

7) Myöhään illalla pitkä nuori mies h kävelee vaakasuoran suoran jalkakäytävän reunaa pitkin tasaisella nopeudella v. Etäisyydellä l Jalkakäytävän reunalta on lyhtypylväs. Palava lyhty on kiinnitetty korkeuteen H maan pinnalta. Muodosta kuvaaja ihmisen pään varjon liikenopeudesta koordinaatista riippuen x. [ratkaisu ]