Semjonov Vlad, Ivasiro Alexander, studenti 9. třídy

Práce a prezentace pro řešení grafických problémů. Byla vyrobena elektronická hra a brožura s grafickými úkoly

Stažení:

Náhled:

Chcete-li používat náhledy prezentací, vytvořte si účet Google a přihlaste se k němu: https://accounts.google.com

Popisky snímků:

teze Řešení problémů je jednou z metod pochopení vzájemného propojení přírodních zákonů. Řešení problémů je jedním z důležitých prostředků opakování, upevňování a sebetestování znalostí. Většinu fyzikálních problémů řešíme analyticky, ale ve fyzice existují problémy, které vyžadují grafické řešení nebo ve kterých je uveden graf. Tyto úlohy vyžadují využití schopnosti číst a analyzovat graf.

Relevance tématu. 1) Řešení a analýza grafických problémů vám umožní pochopit a zapamatovat si základní fyzikální zákony a vzorce. 2) V KIM pro Jednotnou státní zkoušku z fyziky a matematiky jsou zahrnuty úlohy s grafickým obsahem

Cíl projektu: 1. Vydat manuál pro samoučení při řešení grafických problémů. 2. Vytvořte elektronickou hru. Úkoly: 1. Vyberte grafické úkoly na různá témata. 2. Zjistěte obecný vzorec při řešení grafických problémů.

Čtení grafu Stanovení tepelných procesů Stanovení periody, amplitudy, ... Stanovení Ek, Er

V průběhu fyziky 7-9 lze vyzdvihnout zákony, které jsou vyjádřeny přímou závislostí: X(t), m (ρ), I (q), F řízení (Δ x), F tr(N), F ( m), P ( v) , p (F) p (h) , F а(V t) …, kvadratická závislost: E к =mv 2 /2 E р =CU 2 /2 E р =kx 2 /2

1. Porovnejte kapacitu kondenzátorů 2.Který z níže uvedených bodů na diagramu závislosti hybnosti tělesa na jeho hmotnosti odpovídá minimální rychlosti? Podívejme se na problémy 3 1 2

1.Jaký je vztah mezi koeficienty tuhosti? 2. Těleso, které je v počátečním okamžiku v klidu, se pohybuje vlivem konstantní síly, jak je znázorněno na obrázku. Určete velikost průmětu této síly, je-li hmotnost tělesa 3 kg.

Upozorňuji, že je dáno P(V) a otázka se týká Ek 1. Ve kterém z následujících vztahů jsou kinetické energie tří těles různých hmotností v době, kdy jsou jejich rychlosti stejné? 2. Na základě projekce posunu v závislosti na čase pro těleso o hmotnosti 2 kg určete hybnost tělesa v čase 2 s. (Počáteční rychlost je nulová.)

1. Který z následujících grafů nejpřesněji znázorňuje vztah mezi projektovanou rychlostí a časem? (Počáteční rychlost je nulová.) E Od jedné závislosti ke druhé Od grafu ke grafu

2. Těleso o hmotnosti 1 kg mění svůj průmět rychlosti, jak je znázorněno na obrázku. Který z následujících grafů projekce síly v závislosti na čase odpovídá tomuto pohybu?

V kurzu fyziky jsou problémy s několika způsoby řešení: 1. Vypočítejte průměrnou rychlost 2. Určete vztah mezi průměty pohybu těles v okamžiku, kdy jsou rychlosti těles stejné. 10 5 0 V,x ; m/s t,s I II III

Metoda č. 1 10 5 0 V,x ; m/s t,c I II III a x= V 2x – V 1x t 2 – t 1 2 S=v 0 t+at 2 /2

Metoda č. 2 10 5 0 Vx; m/s t,s I II III Sx= (V 0 x + Vx) t/ 2

Metoda č. 3 10 5 0 V,x ; m/s t,s I II III S 3 x= 1 *S S 2 x= 2 *S S 1 x: S 2 x: S 3 x= 3: 2: 1 S 1 x= 3 *S

Extra slide Je zřejmé, že třetí metoda řešení nevyžaduje mezivýpočty, proto je rychlejší a tudíž pohodlnější. Pojďme zjistit, v jakých úkolech je takové využití prostoru možné.

Analýza vyřešených problémů ukazuje, že pokud je součin X a Y fyzikální veličina, pak se rovná ploše obrázku omezeného grafem. P=IU, A=Fs S=vt, V=at, v0=0 Δp/t=F, q=It Fa=V ρ g,…. X Y

1. Obrázek ukazuje graf průmětu rychlosti určitého tělesa v závislosti na čase. Určete průmět posunutí a dráhu tohoto tělesa 5 s po zahájení pohybu. Vx; m/s3o-23t; s 5 A) 5 m, 13 m B) 13 m, 5 m C) -1 m, 0 m D) 9 m, -4 m E) 15 m, 5 m

0 4 6 8 1 2 3 4 5 6 t, s V, m/s 2. Určete průměrnou rychlost cyklisty za čas t=6s. Celou cestu po celou dobu S x = S lichoběžník 4,7 m/s

Změna hybnosti tělesa je určena plochou obrázku - obdélník, pokud je síla konstantní, a pravoúhlý trojúhelník, pokud síla závisí lineárně na čase. F t F t t F

3. Největší změna hybnosti tělesa za 2s F t 1 .A 2 .B 3 .C 1 C B A Nápověda: Ft=S f =  p

4.Pomocí závislosti hybnosti tělesa na čase určete výslednou sílu působící na toto těleso. A) 3H B) 8H C) 12H D) 2H E) 16 past P; kg* m/s 6 2 0 2 t; cF= Ap/t=(6-2)/2=2

Mechanická práce Mechanická práce, konstantní ve velikosti a směru síly, se číselně rovná ploše obdélníku. Mechanická práce síly, jejíž velikost závisí na modulu posunutí podle lineárního zákona, se číselně rovná ploše pravoúhlého trojúhelníku. S 0 F F * s = A = S obdélníkový S 0 F A = ​​​​S obdélníkový

5. Obrázek ukazuje závislost síly působící na těleso na posuvu. Určete práci, kterou tato síla vykoná, když se těleso posune o 20 cm. A) 20J. B) 8J. C) 0,8J. D) 40J. E) 0,4 J. past cm až metry

Vypočítejte náboj 4 I,A 6 2 U,B 4 8 12 16 20 24 Vypočítejte odpor Vypočítejte A, Δ Ek po dobu 4 s Vypočítejte Er pružiny

6. Vlivem proměnlivé síly mění těleso o hmotnosti 1 kg v čase svůj průmět rychlosti, jak je znázorněno na obrázku. Je obtížné určit práci výslednice této síly za 8 sekund po zahájení pohybu A) 512J B) 128J C) 112J D) 64J E) 132J A=FS , S= S (t=4c) =32m F=ma, a=(v-v0)t=2 m/s2

závěr Výsledkem naší práce je vydání brožury s grafickými úlohami pro samostatné řešení a vytvoření elektronické hry. Práce se ukázala jako užitečná pro přípravu na Jednotnou státní zkoušku i pro studenty se zájmem o fyziku. Do budoucna úvahy o jiných typech problémů a jejich řešení.

Funkční závislosti fyzikálních veličin. Obecné metody, techniky a pravidla přístupu k řešení grafických problémů projekt „TALKING LINE“ MBOU Střední škola č. 8 Južno-Sachalinsk Vypracovali: Semjonov Vladislav, Ivasiro Alexander, studenti 9. ročníku „A“

Informační zdroje. 1. Lukashik V.I., Ivanova E.V. Sbírka úloh z fyziky. Moskva „Osvícení“ 2000 2. Stepanova G.I Sbírka úloh z fyziky M. Enlightenment 1995 3. Rymkevich A.P Sbírka úloh z fyziky Moskva. Education 1988. 4. www.afportal.ru 5. A.V. Peryshkin, E.M. Gutnik Učebnice fyziky pro ročníky 7, 8, 9. 6. Materiály GIA 7. S.E. Kamenetsky, V.P. Orekhov Metody řešení problémů ve fyzice na střední škole. M: Vzdělávání, 1987. 8. V.A. Balazsovy problémy ve fyzice a metody jejich řešení. Moskva "osvícení" 1983

Odborníci dokazují výhodu technického vzdělání před humanitními, dokazují, že Rusko nutně potřebuje vysoce kvalifikované inženýry a technické specialisty a tento trend bude pokračovat nejen v roce 2014, ale i v následujících letech. Podle specialistů na výběr personálu, pokud země očekává ekonomický růst v příštích letech (a jsou pro to předpoklady), pak je velmi pravděpodobné, že ruská vzdělávací základna nebude schopna zvládnout mnoho sektorů (špičkové technologie, průmysl) . "V tuto chvíli je na trhu práce akutní nedostatek specialistů v oblasti strojírenství a technických specializací, v oblasti IT: programátoři, softwaroví vývojáři. V poptávce zůstávají inženýři téměř všech specializací. trh je přesycen právníky, ekonomy, novináři, psychology,“ říká generální ředitelka Personální agentury pro jedinečné specialisty Ekaterina Krupina. Analytici, kteří vytvářejí dlouhodobé předpovědi do roku 2020, jsou přesvědčeni, že poptávka po technických specialitách bude každým rokem rychle růst. Relevance problému. Proto je důležitá kvalita přípravy na Jednotnou státní zkoušku z fyziky. Zvládnutí metod řešení fyzikálních problémů je zásadní. Různé fyzické úlohy jsou grafické úlohy. 1) Řešení a analýza grafických problémů vám umožní pochopit a zapamatovat si základní fyzikální zákony a vzorce. 2) V KIM pro Jednotnou státní zkoušku z fyziky jsou zahrnuty úlohy s grafickým obsahem.

Stáhněte si práci s prezentací.

CÍL PROJEKTOVÉ PRÁCE:

Studium typů grafických problémů, odrůd, vlastností a metod řešení .

CÍLE PRÁCE:

1. Prostudování literatury o grafických úlohách; 2. Studium materiálů jednotné státní zkoušky (rozšířenost a míra složitosti grafických úloh); 3. Studium obecných a specifických grafických problémů z různých odvětví fyziky, stupeň složitosti. 4. Studium metod řešení; 5. Provedení sociologického průzkumu mezi studenty a učiteli školy.

Fyzikální problém

V metodicko-naučné literatuře jsou výchovné fyzikální úlohy chápány jako vhodně zvolená cvičení, jejichž hlavním účelem je studovat fyzikální jevy, utvářet pojmy, rozvíjet fyzické myšlení žáků a vštěpovat jim schopnost aplikovat své znalosti v praxi.

Naučit studenty řešit fyzikální problémy je jedním z nejobtížnějších pedagogických problémů. Myslím, že tento problém je velmi aktuální. Můj projekt má za cíl vyřešit dva problémy:

1. Pomoc při výuce žáků ve schopnosti řešit grafické problémy;

2. Zapojte studenty do tohoto typu práce.

Řešení a analýza problému vám umožní porozumět a zapamatovat si základní zákony a vzorce fyziky, vytvořit si představu o jejich charakteristických rysech a limitech použití. Problémy rozvíjejí dovednosti v používání obecných zákonitostí materiálního světa k řešení konkrétních problémů praktického a vzdělávacího významu. Schopnost řešit problémy je nejlepším kritériem pro posouzení hloubky studia programového materiálu a jeho asimilace.

Ve studiích, které zjišťovaly, do jaké míry studenti zvládli jednotlivé operace zahrnuté do schopnosti řešit problémy, bylo zjištěno, že 30–50 % studentů v různých třídách uvádí, že jim takové dovednosti chybí.

Neschopnost řešit problémy je jedním z hlavních důvodů snížené úspěšnosti ve studiu fyziky. Studie ukázaly, že neschopnost samostatně řešit problémy je hlavním důvodem nepravidelného plnění domácích úkolů. Jen malá část studentů ovládá schopnost řešit problémy, což považuje za jednu z nejdůležitějších podmínek pro zkvalitnění znalostí ve fyzice.

Tento stav učební praxe lze vysvětlit nedostatkem jasných požadavků na utváření této dovednosti, nedostatkem vnitřní motivace a kognitivního zájmu mezi studenty.

Řešení problémů v procesu výuky fyziky má mnohostranné funkce:

• Zvládnutí teoretických znalostí.
• Zvládnutí pojmů fyzikálních jevů a veličin.
• Duševní rozvoj, kreativní myšlení a speciální schopnosti žáků.
• Seznamuje studenty s úspěchy vědy a techniky.
• Rozvíjí tvrdou práci, vytrvalost, vůli, charakter a odhodlání.
• Jde o prostředek sledování znalostí, dovedností a schopností žáků.

Grafický úkol.

Grafické úlohy jsou takové úlohy, při jejichž řešení se používají grafy, diagramy, tabulky, výkresy a diagramy.

Například:

1. Sestrojte graf dráhy rovnoměrného pohybu, jestliže v = 2 m/s nebo rovnoměrně zrychleného pohybu, jestliže v 0 = 5 m/sa a = 3 m/s 2 .

2. Jaké jevy charakterizují jednotlivé části grafu...

3. Které těleso se pohybuje rychleji

4. Ve které oblasti se tělo pohybovalo rychleji?

5. Určete ujetou vzdálenost z grafu rychlosti.

6. V jaké části pohybu bylo tělo v klidu. Rychlost se zvyšovala a snižovala.

Řešení grafických problémů pomáhá pochopit funkční vztah mezi fyzikálními veličinami, rozvíjet dovednosti práce s grafy a rozvíjet schopnost práce s měřítky.

Na základě úlohy grafů při řešení problémů je lze rozdělit na dva typy: - problémy, jejichž odpověď na otázku lze nalézt jako výsledek sestrojení grafu; - úkoly, na které lze najít odpověď analýzou grafu.

Grafické úlohy lze kombinovat s experimentálními.

Například:

Pomocí kádinky naplněné vodou určete hmotnost dřevěného špalku...

Příprava na řešení grafických problémů.

Pro řešení grafických úloh musí student znát různé typy funkčních závislostí, což znamená průnik grafů s osami a grafů mezi sebou. Musíte pochopit, jak se liší závislosti, například x = x 0 + vt a x = v 0 t + při 2 /2 nebo x = x m sinω 0 t a x = - x m sinω 0 t; x =x m sin(ω 0 t+ α) a x =x m cos (ω 0 t+ α) atd.

Plán přípravy by měl obsahovat následující části:

· a) Zopakujte si grafy funkcí (lineární, kvadratické, mocninné) · b) Zjistěte, jakou roli hrají grafy ve fyzice, jakou informaci nesou. · c) Systematizovat fyzikální problémy podle významu grafů v nich. · d) Studovat metody a techniky analýzy fyzikálních grafů · e) Vyvinout algoritmus pro řešení grafických problémů v různých odvětvích fyziky · f) Zjistit obecný vzorec při řešení grafických problémů. Pro zvládnutí metod řešení problémů je nutné vyřešit velké množství různých typů problémů, dodržující zásadu - „Od jednoduchých po složité“. Počínaje jednoduchými, osvojit si metody řešení, porovnávat, zobecňovat různé problémy jak na základě grafů, tak na tabulkách, diagramech, diagramech. Měli byste věnovat pozornost označení veličin podél souřadnicových os (jednotky fyzikálních veličin, přítomnost vícenásobných nebo vícenásobných předpon), stupnici, typu funkční závislosti (lineární, kvadratická, logaritmická, trigonometrická atd.), úhly sklonu grafů, průsečíky grafů se souřadnicovými osami nebo grafy mezi sebou. Zvláště opatrně je třeba přistupovat k problémům s vlastními „chybami“, stejně jako k problémům s fotografiemi měřítek měřicích přístrojů. V tomto případě je nutné správně určit hodnotu dělení měřicích přístrojů a přesně odečíst hodnoty měřených veličin. V problémech týkajících se geometrické optiky je zvláště důležité pečlivě a přesně konstruovat paprsky a určit jejich průsečíky s osami a mezi sebou navzájem.

Jak řešit problémy s grafikou

Zvládnutí obecného algoritmu pro řešení fyzikálních úloh

1. Provedení analýzy problémových stavů s identifikací systémových úloh, jevů a procesů popsaných v problému, se stanovením podmínek jejich vzniku

2. Kódování podmínek problému a procesu řešení na různých úrovních:

a) stručný popis problémových podmínek;

b) vytváření výkresů a elektrických schémat;

c) provádění kreseb, grafů, vektorových diagramů;

d) sepsání rovnice (systému rovnic) nebo sestrojení logického závěru

3. Identifikace vhodné metody a metod řešení konkrétního problému

4. Aplikace obecného algoritmu pro řešení problémů různého typu

Řešení problému začíná čtením podmínek. Musíte se ujistit, že všechny termíny a pojmy v podmínce jsou studentům jasné. Nejasné pojmy jsou vyjasněny po prvním přečtení. Zároveň je třeba vyzdvihnout, jaký jev, proces nebo vlastnost těles je v problému popisován. Poté se problém přečte znovu, ale se zvýrazněnými údaji a požadovanými veličinami. A teprve poté se provede krátký záznam podmínek problému.

Plánování

Působení orientace umožňuje sekundární analýzu vnímaných podmínek úkolu, v jejímž důsledku jsou identifikovány fyzikální teorie, zákony, rovnice, které vysvětlují konkrétní úkol. Poté jsou identifikovány metody řešení problémů jedné třídy a nalezena optimální metoda řešení tohoto problému. Výsledkem činnosti žáka je plán řešení, který zahrnuje řetězec logických akcí. Sleduje se správnost akcí k vypracování plánu řešení problému.

Proces řešení

Nejprve je nutné si ujasnit obsah již známých akcí. Působení orientace v této fázi zahrnuje opět zdůraznění způsobu řešení problému a objasnění typu problému, který má být řešen metodou stanovení podmínek. Dalším krokem je plánování. Je plánována metoda řešení problému, aparatura (logická, matematická, experimentální), pomocí které je možné provádět jeho další řešení.

Analýza řešení

Poslední fází procesu řešení problému je kontrola získaného výsledku. Provádí se opět stejnými akcemi, ale mění se obsah akcí. Akce orientace je zjištění podstaty toho, co je třeba zkontrolovat. Výsledkem řešení mohou být například hodnoty koeficientů, fyzikální konstantní charakteristiky mechanismů a strojů, jevů a procesů.

Výsledek získaný řešením problému musí být věrohodný a v souladu se zdravým rozumem.

Převaha grafických úloh v počítačových simulačních strojích v úlohách jednotné státní zkoušky

Studium materiálů k jednotné státní zkoušce po řadu let (2004 - 2013) ukázalo, že grafické problémy v různých oblastech fyziky jsou běžné v zadáních jednotných státních zkoušek v různých oblastech fyziky. V úlohách A: z mechaniky - 2-3 z molekulární fyziky - 1 z termodynamiky - 3 z elektrodynamiky - 3-4 z optiky - 1-2 z kvantové fyziky - 1 z atomové a jaderné fyziky - 1 V úlohách B: z mechaniky - 1 z molekulární fyziky - 1 z termodynamiky - 1 z elektrodynamiky - 1 z optiky - 1 z kvantové fyziky - 1 z atomové a jaderné fyziky - 1 z úloh C: z mechaniky - z molekulární fyziky - z termodynamiky - 1 z elektrodynamiky - 1 z optika - 1 z kvantové fyziky - z atomové a jaderné fyziky - 1

Náš výzkum

A. Analýza chyb při řešení grafických problémů

Analýza řešení grafických problémů ukázala, že se vyskytují následující běžné chyby:

Chyby při čtení grafů;

Chyby v operacích s vektorovými veličinami;

Chyby při analýze izoprocesních grafů;

Chyby v grafické závislosti elektrických veličin;

Chyby při konstrukci pomocí zákonů geometrické optiky;

Chyby v grafických úlohách o kvantových zákonech a fotoelektrickém jevu;

Chyby v aplikaci zákonů atomové fyziky.

B. Sociologický průzkum

Abychom zjistili, jak si žáci školy uvědomují grafické úlohy, provedli jsme sociologický průzkum.

Žákům a učitelům naší školy jsme položili následující otázky: profily:

1. 1. Co je to grafický úkol?

a) problémy s obrázky;

b) úlohy obsahující diagramy, diagramy;

c) Nevím.

1. 2. K čemu jsou grafické úlohy?

b) rozvíjet schopnost vytvářet grafy;

c) Nevím.

3. Dokážete vyřešit grafické problémy?

a) ano; b) ne; c) nejsem si jistý ;

4. Chcete se naučit řešit grafické problémy?

A) ano ; b) ne; c) Je pro mě těžké odpovědět.

Dotazováno bylo 50 lidí. Na základě průzkumu byly získány následující údaje:

ZÁVĚRY:

1. V důsledku práce na projektu „Graphical Tasks“ jsme studovali vlastnosti grafických úloh.
2. Studovali jsme vlastnosti metodiky řešení grafických problémů.
3. Analyzovali jsme typické chyby.
4. Provedl sociologický průzkum.

Reflexe aktivity:

1. Bylo pro nás zajímavé pracovat na problému grafických úloh.
2. Naučili jsme se, jak provádět výzkum, porovnávat a porovnávat výsledky výzkumu.
3. Zjistili jsme, že pro pochopení fyzikálních jevů je nezbytné zvládnutí metod pro řešení grafických problémů.
4. Zjistili jsme, že pro úspěšné složení jednotné státní zkoušky je nutné zvládnutí metod řešení grafických problémů.

Pokud má problém lineárního programování pouze dvě proměnné, lze jej vyřešit graficky.

Zvažte problém lineárního programování se dvěma proměnnými a:
(1.1) ;
(1.2)
Zde jsou libovolná čísla. Úkolem může být buď najít maximum (max), nebo najít minimum (min). Systém omezení může obsahovat jak značky, tak značky.

Konstrukce domény proveditelných řešení

Grafická metoda řešení problému (1) je následující.
Nejprve si nakreslíme souřadnicové osy a vybereme měřítko. Každá z nerovností soustavy vazeb (1.2) definuje polorovinu ohraničenou příslušnou přímkou.

Takže první nerovnost
(1.2.1)
definuje polorovinu ohraničenou přímkou. Na jedné straně této přímky a na druhé straně. Na velmi rovné čáře. Abychom zjistili, na které stranové nerovnosti (1.2.1) platí, zvolíme libovolný bod, který na přímce neleží. Dále dosadíme souřadnice tohoto bodu do (1.2.1). Pokud nerovnost platí, pak polorovina obsahuje vybraný bod. Pokud nerovnice neplatí, pak se polorovina nachází na druhé straně (neobsahuje vybraný bod). Vystínujte polorovinu, pro kterou platí nerovnost (1.2.1).

Totéž uděláme pro zbývající nerovnosti soustavy (1.2). Takto získáme zastíněné poloroviny. Body oblasti proveditelných řešení splňují všechny nerovnosti (1.2). Proto je graficky oblast proveditelných řešení (ADA) průsečíkem všech sestrojených polorovin. Stínování ODR. Je to konvexní mnohoúhelník, jehož plochy patří k sestrojeným přímkám. ODF může být také neomezená konvexní postava, segment, paprsek nebo přímka.

Může také nastat případ, že poloroviny neobsahují společné body. Pak doménou proveditelných řešení je prázdná množina. Tento problém nemá řešení.

Metodu lze zjednodušit. Nemusíte stínovat každou polorovinu, ale nejprve vytvořte všechny rovné čáry
(2)
Dále vyberte libovolný bod, který nepatří do žádné z těchto čar. Dosadíme souřadnice tohoto bodu do soustavy nerovnic (1.2). Pokud jsou splněny všechny nerovnosti, pak je oblast proveditelných řešení omezena sestrojenými přímkami a zahrnuje vybraný bod. Oblast proveditelných řešení vystínujeme podél hranic čar tak, aby zahrnovala vybraný bod.

Pokud není splněna alespoň jedna nerovnost, vyberte jiný bod. A tak dále, dokud není nalezen jeden bod, jehož souřadnice vyhovují systému (1.2).

Nalezení extrému účelové funkce

Máme tedy zastíněnou oblast proveditelných řešení (ADA). Je omezena přerušovanou čarou sestávající ze segmentů a paprsků patřících do sestrojených přímek (2). ODS je vždy konvexní množina. Může to být buď omezená množina, nebo neomezená v některých směrech.

Nyní můžeme hledat extrém účelové funkce
(1.1) .

Chcete-li to provést, vyberte libovolné číslo a vytvořte přímku
(3) .
Pro usnadnění další prezentace předpokládáme, že tato přímka prochází ODR. Na tomto řádku je účelová funkce konstantní a rovna . taková přímka se nazývá čára funkční úrovně. Tato přímka rozděluje rovinu na dvě poloroviny. Na jedné polorovině
.
Na další polorovině
.
To znamená, že na jedné straně přímky (3) se účelová funkce zvyšuje. A čím dále posuneme bod od přímky (3), tím větší bude hodnota. Na druhé straně přímky (3) se účelová funkce snižuje. A čím dále posuneme bod od přímky (3) na druhou stranu, tím menší bude hodnota. Pokud nakreslíme přímku rovnoběžnou s přímkou ​​(3), pak nová přímka bude také úrovňovou přímkou ​​účelové funkce, ale s jinou hodnotou.

Abychom tedy našli maximální hodnotu účelové funkce, je nutné nakreslit přímku rovnoběžnou s přímkou ​​(3), co nejdále od ní ve směru rostoucích hodnot a procházející alespoň jedním bodem. z ODD. Pro zjištění minimální hodnoty účelové funkce je nutné nakreslit přímku rovnoběžnou s přímkou ​​(3) a co nejdále od ní ve směru klesajících hodnot a procházející alespoň jedním bodem ODD.

Pokud je ODR neomezené, pak může nastat případ, kdy takovou přímou linku nelze čerpat. Tzn., že ať odstraníme přímku z nivelační čáry (3) ve směru zvyšování (klesání), přímka bude vždy procházet ODR. V tomto případě může být libovolně velký (malý). Neexistuje tedy žádná maximální (minimální) hodnota. Problém nemá řešení.

Uvažujme případ, kdy krajní přímka rovnoběžná s libovolnou přímkou ​​tvaru (3) prochází jedním vrcholem polygonu ODR. Z grafu určíme souřadnice tohoto vrcholu. Potom je maximální (minimální) hodnota účelové funkce určena vzorcem:
.
Řešením problému je
.

Může také nastat případ, kdy je přímka rovnoběžná s jednou ze stran ODR. Poté přímka prochází dvěma vrcholy polygonu ODR. Určíme souřadnice těchto vrcholů. K určení maximální (minimální) hodnoty účelové funkce můžete použít souřadnice kteréhokoli z těchto vrcholů:
.
Problém má nekonečně mnoho řešení. Řešením je libovolný bod umístěný na segmentu mezi body a , včetně bodů a samotných.

Příklad řešení úlohy lineárního programování pomocí grafické metody

Úkol

Společnost vyrábí šaty dvou modelů A a B. Používají se tři druhy látek. Na zhotovení jedněch šatů modelu A jsou potřeba 2 m látky prvního typu, 1 m látky druhého typu, 2 m látky třetího typu. Na zhotovení jedněch šatů modelu B jsou potřeba 3 m látky prvního typu, 1 m látky druhého typu, 2 m látky třetího typu. Zásoby tkaniny prvního typu jsou 21 m, druhého typu 10 m, třetího typu 16 m. Vydání jednoho výrobku typu A přináší příjem 400 den. jednotek, jeden výrobek typ B - 300 den. Jednotky

Vypracujte plán výroby, který zajistí společnosti největší příjmy. Vyřešte problém graficky.

Řešení

Nechte proměnné a označte počet vyrobených šatů, modely A a B. Potom množství spotřebované látky prvního typu bude:
(m)
Množství spotřebované látky druhého typu bude:
(m)
Množství spotřebované látky třetího typu bude:
(m)
Vzhledem k tomu, že počet vyrobených šatů nemůže být záporný
A .
Příjem z vyrobených šatů bude:
(den. jednotky)

Pak má ekonomicko-matematický model problému tvar:

Řešíme to graficky.
Nakreslíme souřadnicové osy a .

Stavíme přímku.
Na .
Na .
Nakreslete přímku skrz body (0; 7) a (10,5; 0).

Stavíme přímku.
Na .
Na .
Nakreslete přímku skrz body (0; 10) a (10; 0).

Stavíme přímku.
Na .
Na .
Nakreslete přímku skrz body (0; 8) a (8; 0).

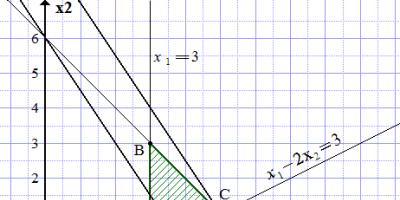
Plochu vystínujeme tak, aby bod (2; 2) spadal do zastíněné části. Získáme čtyřúhelník OABC.

(A1.1) .
Na .
Na .
Nakreslete přímku skrz body (0; 4) a (3; 0).

Dále poznamenáváme, že protože koeficienty a účelové funkce jsou kladné (400 a 300), zvyšuje se a zvyšuje. Vedeme přímku rovnoběžnou s přímkou ​​(A1.1), co nejdále od ní ve směru rostoucí a procházející alespoň jedním bodem čtyřúhelníku OABC. Taková přímka prochází bodem C. Z konstrukce určíme její souřadnice.
.

Řešení problému: ;

Odpovědět

.
To znamená, že pro získání co největšího příjmu je potřeba vyrobit 8 šatů modelu A. Příjem bude 3200 den. Jednotky

Příklad 2

Úkol

Řešte úlohu lineárního programování graficky.

Řešení

Řešíme to graficky.
Nakreslíme souřadnicové osy a .

Stavíme přímku.
Na .
Na .
Nakreslete přímku skrz body (0; 6) a (6; 0).

Stavíme přímku.
Odtud.
Na .
Na .
Nakreslete přímku přes body (3; 0) a (7; 2).

Stavíme přímku.
Postavíme přímku (osa úsečky).

Oblast přípustných řešení (ADA) je omezena sestrojenými přímkami. Abychom zjistili, na kterou stranu, všimneme si, že bod patří do ODR, protože vyhovuje systému nerovností:

Plochu podél hranic sestrojených čar vystínujeme tak, aby bod (4; 1) spadal do stínované části. Dostaneme trojúhelník ABC.

Postavíme libovolnou linii úrovně účelové funkce, např.
.
Na .
Na .
Nakreslete rovnou linii přes body (0; 6) a (4; 0).
Protože účelová funkce roste s rostoucí a , vedeme přímku rovnoběžnou s linií hladiny a co nejdále od ní ve směru rostoucí a procházející alespoň jedním bodem trojúhelníku ABC. Taková přímka prochází bodem C. Z konstrukce určíme její souřadnice.
.

Řešení problému: ;

Odpovědět

Příklad žádného řešení

Úkol

Řešte úlohu lineárního programování graficky. Najděte maximální a minimální hodnotu účelové funkce.

Řešení

Problém řešíme graficky.
Nakreslíme souřadnicové osy a .

Stavíme přímku.
Na .
Na .
Nakreslete přímku skrz body (0; 8) a (2,667; 0).

Stavíme přímku.
Na .
Na .
Nakreslete přímku skrz body (0; 3) a (6; 0).

Stavíme přímku.
Na .
Na .
Nakreslete přímku přes body (3; 0) a (6; 3).

Přímky jsou souřadnicové osy.

Oblast přípustných řešení (ADA) je omezena sestrojenými přímkami a souřadnými osami. Abychom zjistili, na kterou stranu, všimneme si, že bod patří do ODR, protože vyhovuje systému nerovností:

Plochu vystínujeme tak, aby bod (3; 3) spadal do zastíněné části. Získáme neohraničenou plochu ohraničenou přerušovanou čárou ABCDE.

Postavíme libovolnou linii úrovně účelové funkce, např.
(A3.1) .
Na .
Na .
Nakreslete přímku přes body (0; 7) a (7; 0).
Protože koeficienty a jsou kladné, roste s rostoucím a .

Chcete-li najít maximum, musíte nakreslit rovnoběžku, která je co nejdále ve směru růstu a prochází alespoň jedním bodem oblasti ABCDE. Protože je však oblast neomezená na straně velkých hodnot a , nelze takovou přímku nakreslit. Bez ohledu na to, jakou čáru nakreslíme, vždy budou v regionu body vzdálenější ve směru nárůstu a . Proto neexistuje žádné maximum. můžete to udělat tak velký, jak chcete.

Hledáme minimum. Vedeme přímku rovnoběžnou s přímkou ​​(A3.1) a co nejdále od ní ve směru klesající a procházející alespoň jedním bodem oblasti ABCDE. Taková přímka prochází bodem C. Z konstrukce určíme její souřadnice.
.
Minimální hodnota účelové funkce:

Odpovědět

Neexistuje žádná maximální hodnota.
Minimální hodnota
.

Grafické znázornění fyzikálního procesu jej často činí vizuálnějším, a tím usnadňuje pochopení uvažovaného jevu. Grafy, které někdy umožňují výrazně zjednodušit výpočty, jsou v praxi široce používány k řešení různých problémů. Schopnost je sestavit a přečíst je dnes pro mnoho specialistů povinná.

Za grafické úlohy považujeme následující úlohy:

• pro stavebnictví, kde jsou výkresy a výkresy velmi užitečné;
• schémata řešená pomocí vektorů, grafů, diagramů, diagramů a nomogramů.

1) Míč je vyhozen svisle nahoru ze země počáteční rychlostí protiÓ. Nakreslete graf závislosti rychlosti míče na čase za předpokladu, že dopady na zem jsou dokonale elastické. Zanedbávejte odpor vzduchu. [řešení ]

2) Cestující, který měl zpoždění na vlak, si všiml, že ho předposlední vůz projel ti = 10 s, a poslední - pro t2 = 8 s. Za předpokladu, že se pohyb vlaku rovnoměrně zrychluje, určete dobu zpoždění. [řešení ]

3) V místnosti vysoko H na jednom konci je ke stropu připevněna lehká pružina s tuhostí k, mající délku v nedeformovaném stavu hle (hle< H ). Na podlaze pod pružinou je umístěn blok výšky X se základní plochou S, vyrobený z materiálu s hustotou ρ . Sestrojte graf tlaku kvádru na podlahu v závislosti na výšce kvádru. [řešení ]

4) Štěnice se plazí podél osy Vůl. Určete průměrnou rychlost jeho pohybu v oblasti mezi body se souřadnicemi x 1 = 1,0 m A x 2 = 5,0 m pokud je známo, že součin rychlosti hmyzu a jeho souřadnic zůstává po celou dobu konstantní, rovna c = 500 cm2/s. [řešení ]

5) Do bloku hmoty 10 kg na vodorovnou plochu působí síla. Vzhledem k tomu, že koeficient tření je roven 0,7 , definovat:

• třecí síla pro případ, kdyby F = 50 N a směrováno vodorovně.
• třecí síla pro případ, kdyby F = 80 N a směrováno vodorovně.
• nakreslete graf zrychlení bloku proti horizontálně působící síle.
• Jaká je minimální síla potřebná k vytažení lana, aby se blok pohyboval rovnoměrně? [řešení ]

6) Ke směšovači jsou připojeny dvě trubky. Každé potrubí má kohoutek, kterým lze regulovat průtok vody potrubím a měnit jej z nuly na maximální hodnotu Jo = 1 l/s. Voda proudí v potrubí při teplotách ti = 10 °C A t2 = 50 °C. Nakreslete graf maximálního průtoku vody vytékající z mixéru v závislosti na teplotě této vody. Tepelné ztráty zanedbávejte. [řešení ]

7) Pozdě večer vysoký mladý muž h jde po okraji vodorovného rovného chodníku konstantní rychlostí proti. Na dálku l Z okraje chodníku je kandelábr. Hořící lucerna je upevněna ve výšce H z povrchu země. Sestrojte graf rychlosti pohybu stínu hlavy člověka v závislosti na souřadnici X. [řešení ]