Semyonov Vlad, Ivasiro Alexander, elever i 9:e klass

Arbete och presentation för att lösa grafiska problem. Ett elektroniskt spel och en broschyr med grafiska uppgifter gjordes

Ladda ner:

Förhandsvisning:

För att använda presentationsförhandsvisningar, skapa ett Google-konto och logga in på det: https://accounts.google.com

Bildtexter:

avhandling Problemlösning är en av metoderna för att förstå kopplingen mellan naturlagarna. Att lösa problem är ett av de viktiga medlen för upprepning, konsolidering och självtestning av kunskap. Vi löser de flesta fysiska problem analytiskt, men inom fysiken finns det problem som kräver en grafisk lösning eller där en graf presenteras. Dessa uppgifter kräver användning av förmågan att läsa och analysera en graf.

Ämnets relevans. 1) Genom att lösa och analysera grafiska problem kan du förstå och komma ihåg fysikens grundläggande lagar och formler. 2) I KIMs för Unified State Examination i fysik och matematik ingår uppgifter med grafiskt innehåll

Projektmål: 1. Att ge ut en manual för självlärande vid lösning av grafiska problem. 2. Skapa ett elektroniskt spel. Uppgifter: 1. Välj grafiska uppgifter om olika ämnen. 2. Ta reda på det allmänna mönstret för att lösa grafiska problem.

Läsa en graf Bestämning av termiska processer Bestämning av period, amplitud, ... Bestämning av Ek, Er

I fysik 7-9 kan man lyfta fram lagar som uttrycks genom direkt beroende: X(t), m (ρ), I (q), F kontroll(Δ x), F tr(N), F ( m), P ( v) , p (F) p (h) , F а(V t) …, kvadratiskt beroende: E к =mv 2 /2 E р =CU 2 /2 E р =kx 2 /2

1 . Jämför kondensatorernas kapacitans 2.Vilka av punkterna som anges nedan på diagrammet över beroendet av en kropps rörelsemängd av dess massa motsvarar minimihastigheten? Låt oss överväga problem 3 1 2

1.Vad är sambandet mellan styvhetskoefficienterna? 2. Kroppen, som är i vila i det första ögonblicket, rör sig under inverkan av en konstant kraft som visas i figuren. Bestäm storleken på projektionen av denna kraft om kroppsmassan är 3 kg.

Observera att P(V) ges, och frågan handlar om Ek 1. I vilka av följande samband finns kinetiska energier för tre kroppar med olika massor vid en tidpunkt då deras hastigheter är desamma? 2. Baserat på projektionen av förskjutning mot tid för en kropp som väger 2 kg, bestäm kroppens rörelsemängd vid tidpunkten 2 s. (Starthastigheten är noll.)

1 . Vilken av följande grafer representerar mest exakt förhållandet mellan projicerad hastighet och tid? (Initialhastigheten är noll.) E Från ett beroende till ett annat Från graf till graf

2. En kropp med massan 1 kg ändrar sin hastighetsprojektion som visas i figuren. Vilken av följande grafer över kraftprojektion mot tid motsvarar denna rörelse?

I en fysikkurs finns det problem med flera lösningsmetoder: 1. Beräkna medelhastigheten 2. Bestäm förhållandet mellan projektionerna av kroppars rörelse i det ögonblick då kropparnas hastigheter är desamma. 1050 V,x; m/s t,s I II III

Metod nr 1 10 5 0 V,x ; m/s t,c I II III a x= V 2x – V 1x t 2 – t 1 2 S=v 0 t+at 2 /2

Metod nr 2 10 5 0 Vx; m/s t,s I II III Sx= (V 0 x + Vx) t/ 2

Metod nr 3 10 5 0 V,x ; m/s t,s I II III S 3 x= 1 *S S 2 x= 2 *S S 1 x: S 2 x: S 3 x= 3: 2: 1 S 1 x= 3 *S

Extra slide Självklart kräver den tredje lösningsmetoden inte mellanliggande beräkningar, därför är den snabbare och därför mer bekväm. Låt oss ta reda på i vilka uppgifter sådan användning av utrymme är möjlig.

Analys av lösta problem visar att om produkten av X och Y är en fysisk storhet, så är den lika med den yta av figuren som begränsas av grafen. P=IU, A=Fs S=vt, V=at, v 0 =0 Δp/t=F, q=It Fa=V ρg,…. X Y

1. Figuren visar en graf över projektionen av en viss kropps hastighet mot tiden. Bestäm projektionen av förskjutningen och banan för denna kropp 5 s efter rörelsestart. Vx; m/s 30-23t; s 5 A) 5 m, 13 m B) 13 m, 5 m C) -1 m, 0 m D) 9 m, -4 m E) 15 m, 5 m

0 4 6 8 1 2 3 4 5 6 t, s V, m/s 2. Bestäm cyklistens medelhastighet under tiden t=6s. Hela vägen för hela tiden S x = S trapets 4,7 m/s

Förändringen i en kropps rörelsemängd bestäms av figurens yta - en rektangel om kraften är konstant och en rätvinklig triangel om kraften beror linjärt på tiden. F t F t t F

3. Den största förändringen i en kropps rörelsemängd i 2s F t 1 .A 2 .B 3 .C 1 C B A Tips: Ft=S f =  p

4. Med hjälp av beroendet av kroppens momentum i tid, bestäm den resulterande kraften som verkar på denna kropp. A) 3H B) 8H C) 12H D) 2H E) 16 fälla P; kg* m/s 6 2 0 2 t; c F= A p/t=(6-2)/2=2

Mekaniskt arbete Mekaniskt arbete, konstant i storlek och kraftriktning, är numeriskt lika med rektangelns area. Kraftens mekaniska arbete, vars storlek beror på förskjutningsmodulen enligt en linjär lag, är numeriskt lika med arean av den räta triangeln. S 0 F F * s = A = S rektangulär S 0 F A = S rektangulär

5. Figuren visar beroendet av kraften som verkar på kroppen vid förskjutning. Bestäm arbetet som utförs av denna kraft när kroppen rör sig 20 cm. A) 20J. B) 8J. C) 0,8J. D) 40J. E) 0,4J. fälla cm till meter

Beräkna laddningen 4 I,A 6 2 U,B 4 8 12 16 20 24 Beräkna resistansen Beräkna A, Δ Ek i 4 s Beräkna Er av fjädern

6. Under påverkan av en variabel kraft ändrar en kropp med massan 1 kg sin hastighetsprojektion över tiden, som visas i figuren. Det är svårt att avgöra resultatet av denna krafts arbete inom 8 sekunder efter rörelsens början A) 512J B) 128J C) 112J D) 64J E) 132J A=FS , S= S (t=4c) =32m , F =ma, a =(v-vo)t=2 m/s2

slutsats Som ett resultat av vårt arbete publicerade vi en broschyr med grafiska uppgifter för oberoende lösning och skapade ett elektroniskt spel. Arbetet visade sig vara användbart för att förbereda sig för Unified State Exam, såväl som för studenter intresserade av fysik. I framtiden, övervägande av andra typer av problem och deras lösning.

Funktionella beroenden av fysiska storheter. Allmänna metoder, tekniker och förhållningssätt för att lösa grafiska problem projekt "TALKING LINE" MBOU Secondary School nr 8 Yuzhno-Sakhalinsk Slutförd av: Semyonov Vladislav, Ivasiro Alexander, elever i 9:e klass "A"

Informationskällor. 1. Lukashik V.I., Ivanova E.V. Samling av problem i fysik. Moskva "Enlightenment" 2000 2. Stepanova G.I Samling av problem i fysik M. Upplysning 1995 3. Rymkevich A.P Samling av problem i fysik Moskva. Utbildning 1988. 4. www.afportal.ru 5. A.V. Peryshkin, E.M. Gutnik Fysik lärobok för årskurserna 7, 8, 9. 6. GIA-material 7. S.E. Kamenetsky, V.P. Orekhov Metoder för att lösa problem i fysik i gymnasiet. M: Utbildning, 1987. 8. V.A. Balazs Problem i fysik och metoder för att lösa dem. Moskva "upplysning" 1983

Experter bevisar fördelen med teknisk utbildning framför humaniora, de bevisar att Ryssland är i stort behov av högkvalificerade ingenjörer och tekniska specialister, och denna trend kommer att fortsätta inte bara under 2014 utan även under de kommande åren. Enligt personalvalsspecialister, om landet förväntar sig ekonomisk tillväxt under de kommande åren (och det finns förutsättningar för detta), är det mycket troligt att den ryska utbildningsbasen inte kommer att kunna hantera många sektorer (högteknologi, industri) . "För tillfället råder det en akut brist på specialister på arbetsmarknaden inom området teknik och tekniska specialiteter, inom IT: programmerare, mjukvaruutvecklare. Ingenjörer av nästan alla specialiseringar är fortfarande efterfrågade. Samtidigt, marknaden är övermättad med jurister, ekonomer, journalister, psykologer,” - säger generaldirektör för rekryteringsbyrån för unika specialister Ekaterina Krupina. Analytiker, som gör långsiktiga prognoser fram till 2020, är övertygade om att efterfrågan på tekniska specialiteter kommer att växa snabbt varje år. Problemets relevans. Därför är kvaliteten på förberedelserna för Unified State Exam i fysik viktig. Att bemästra metoder för att lösa fysiska problem är avgörande. En mängd olika fysiska uppgifter är grafiska uppgifter. 1) Genom att lösa och analysera grafiska problem kan du förstå och komma ihåg fysikens grundläggande lagar och formler. 2) I KIM för Unified State Examination i fysik ingår uppgifter med grafiskt innehåll.

Ladda ner arbete med presentation.

MÅL MED PROJEKTARBETE:

Studera typer av grafiska problem, varianter, funktioner och lösningsmetoder .

MÅL FÖR ARBETET:

1. Studera litteratur om grafiska uppgifter; 2. Studie av Unified State Exam-material (prevalens och komplexitetsnivå för grafiska uppgifter); 3. Studie av allmänna och specifika grafiska problem från olika grenar av fysiken, grad av komplexitet. 4. Studie av lösningsmetoder; 5. Genomföra en sociologisk undersökning bland skolelever och lärare.

Fysik problem

I metodisk och pedagogisk litteratur förstås pedagogiska fysiska uppgifter som lämpligt utvalda övningar, vars huvudsakliga syfte är att studera fysiska fenomen, forma begrepp, utveckla elevernas fysiska tänkande och ingjuta i dem förmågan att tillämpa sina kunskaper i praktiken.

Att lära eleverna att lösa fysiska problem är ett av de svåraste pedagogiska problemen. Jag tror att detta problem är mycket relevant. Mitt projekt syftar till att lösa två problem:

1. Hjälp till att lära skolbarn förmågan att lösa grafiska problem;

2. Involvera eleverna i den här typen av arbete.

Genom att lösa och analysera ett problem kan du förstå och komma ihåg fysikens grundläggande lagar och formler, skapa en uppfattning om deras karakteristiska egenskaper och tillämpningsgränser. Problem utvecklar färdigheter i att använda den materiella världens allmänna lagar för att lösa specifika frågor av praktisk och pedagogisk betydelse. Förmågan att lösa problem är det bästa kriteriet för att bedöma studiedjupet av programmaterial och dess assimilering.

I studier för att identifiera i vilken grad eleverna behärskar individuella operationer som ingår i förmågan att lösa problem har det visat sig att 30-50 % av eleverna i olika klasser anger att de saknar sådana färdigheter.

Oförmåga att lösa problem är en av huvudorsakerna till minskad framgång i fysikstudier. Studier har visat att oförmågan att lösa problem självständigt är den främsta orsaken till oregelbundna läxor. Endast en liten del av eleverna behärskar förmågan att lösa problem, vilket de anser vara en av de viktigaste förutsättningarna för att förbättra kvaliteten på kunskaper i fysik.

Detta tillstånd av inlärningspraktik kan förklaras av avsaknaden av tydliga krav för bildandet av denna färdighet, avsaknaden av inre motivation och kognitivt intresse bland eleverna.

Att lösa problem i processen att lära ut fysik har mångfacetterade funktioner:

Att bemästra teoretiska kunskaper.
Att bemästra begreppen fysiska fenomen och kvantiteter.
Mental utveckling, kreativt tänkande och speciella förmågor hos elever.
Introducerar eleverna till prestationer inom vetenskap och teknik.
Utvecklar hårt arbete, uthållighet, vilja, karaktär och beslutsamhet.
Det är ett sätt att övervaka elevernas kunskaper, färdigheter och förmågor.

Grafisk uppgift.

Grafiska uppgifter är de uppgifter i processen att lösa vilka grafer, diagram, tabeller, ritningar och diagram som används.

Till exempel:

1. Konstruera en graf över banan för likformig rörelse om v = 2 m/s eller likformigt accelererad rörelse om v 0 = 5 m/s och a = 3 m/s 2 .

2. Vilka fenomen kännetecknas av varje del av grafen...

3. Vilken kropp rör sig snabbare

4. I vilket område rörde sig kroppen snabbare?

5. Bestäm tillryggalagd sträcka från hastighetsdiagrammet.

6. I vilken del av rörelsen var kroppen i vila. Hastigheten ökade och minskade.

Att lösa grafiska problem hjälper till att förstå det funktionella sambandet mellan fysiska storheter, utveckla färdigheter i att arbeta med grafer och utveckla förmågan att arbeta med skalor.

Baserat på grafernas roll för att lösa problem kan de delas in i två typer: - problem, svaret på frågan om vilka kan hittas som ett resultat av att konstruera en graf; - uppgifter för vilka svaret kan hittas genom att analysera grafen.

Grafiska uppgifter kan kombineras med experimentella.

Till exempel:

Använd en bägare fylld med vatten och bestäm vikten på ett träblock...

Förberedelse för att lösa grafiska problem.

För att lösa grafiska problem ska eleven känna till olika typer av funktionella beroenden, vilket innebär skärningspunkten mellan grafer med axlar och grafer med varandra. Du måste förstå hur beroenden skiljer sig, till exempel x = x 0 + vt och x = v 0 t + vid 2 /2 eller x = x m sinω 0 t och x = - x m sinω 0 t; x =x m sin(ω 0 t+ α) och x =x m cos (ω 0 t+ α), etc.

Förberedelseplanen bör innehålla följande avsnitt:

· a) Upprepa grafer för funktioner (linjär, kvadratisk, potens) · b) Ta reda på vilken roll grafer spelar i fysiken, vilken information de bär. · c) Systematisera fysiska problem efter betydelsen av graferna i dem. · d) Studera metoder och tekniker för att analysera fysiska grafer · e) Utveckla en algoritm för att lösa grafiska problem inom olika grenar av fysiken · f) Ta reda på det allmänna mönstret för att lösa grafiska problem. För att behärska problemlösningsmetoder är det nödvändigt att lösa ett stort antal olika typer av problem, iaktta principen - "Från enkel till komplex." Börja med enkla, behärska lösningsmetoder, jämföra, generalisera olika problem både utifrån grafer och på tabeller, diagram, diagram. Du bör vara uppmärksam på beteckningen av kvantiteter längs koordinataxlarna (enheter av fysiska kvantiteter, närvaron av submultipla eller multipla prefix), skalan, typen av funktionellt beroende (linjär, kvadratisk, logaritmisk, trigonometrisk, etc.), lutningsvinklar för graferna, skärningspunkterna för graferna med koordinataxlar eller grafer sinsemellan. Det är nödvändigt att närma sig problem med inneboende "fel" särskilt noggrant, såväl som problem med fotografier av mätinstrumentsvågar. I det här fallet är det nödvändigt att korrekt bestämma delningsvärdet för mätinstrumenten och noggrant läsa värdena för de uppmätta kvantiteterna. I problem som involverar geometrisk optik är det särskilt viktigt att noggrant och noggrant konstruera strålar och bestämma deras skärningspunkter med axlar och med varandra.

Hur man löser grafikproblem

Att behärska den allmänna algoritmen för att lösa fysiska problem

1. Genomföra en analys av problemförhållandena med identifiering av systemuppgifter, fenomen och processer som beskrivs i problemet, med bestämning av förutsättningarna för deras uppkomst

2. Koda problemförhållandena och lösningsprocessen på olika nivåer:

a) en kort redogörelse för problemförhållandena;

b) att göra ritningar och elektriska diagram;

c) utförande av ritningar, grafer, vektordiagram;

d) skriva en ekvation (ekvationssystem) eller konstruera en logisk slutsats

3. Identifiering av lämplig metod och metoder för att lösa ett specifikt problem

4. Tillämpning av en generell algoritm för att lösa problem av olika slag

Att lösa problemet börjar med att läsa villkoren. Du måste se till att alla termer och begrepp i villkoret är tydliga för eleverna. Otydliga termer förtydligas efter inledande läsning. Samtidigt är det nödvändigt att belysa vilket fenomen, process eller egenskap hos kroppar som beskrivs i problemet. Sedan läses problemet igen, men med data och nödvändiga kvantiteter markerade. Och först efter detta utförs en kort inspelning av villkoren för problemet.

Planera

Orienteringsåtgärden möjliggör en sekundär analys av de upplevda förhållandena för uppgiften, som ett resultat av vilken fysikaliska teorier, lagar, ekvationer som förklarar en specifik uppgift identifieras. Sedan identifieras metoder för att lösa problem i en klass och den optimala metoden för att lösa detta problem hittas. Resultatet av elevaktivitet är en lösningsplan som inkluderar en kedja av logiska åtgärder. Korrektheten av åtgärderna för att upprätta en plan för att lösa problemet övervakas.

Lösningsprocess

Först är det nödvändigt att klargöra innehållet i redan kända åtgärder. Orienteringsåtgärden i detta skede innebär återigen att lyfta fram metoden för att lösa problemet och klargöra vilken typ av problem som ska lösas med metoden att ställa villkoren. Nästa steg är planering. En metod för att lösa problemet planeras, apparaten (logisk, matematisk, experimentell) med hjälp av vilken det är möjligt att utföra dess vidare lösning.

Lösningsanalys

Det sista steget i problemlösningsprocessen är att kontrollera det erhållna resultatet. Det utförs igen av samma åtgärder, men innehållet i åtgärderna ändras. Handlingen av orientering är att ta reda på essensen av det som måste kontrolleras. Till exempel kan resultatet av lösningen vara värdena på koefficienter, fysiska konstanta egenskaper hos mekanismer och maskiner, fenomen och processer.

Resultatet av att lösa problemet måste vara rimligt och överensstämma med sunt förnuft.

Förekomst av grafiska uppgifter i datorsimuleringsmaskiner i Unified State Examination uppgifter

Studien av Unified State Exam-material under ett antal år (2004 - 2013) visade att grafiska problem i olika sektioner av fysiken är vanliga i Unified State Exam-uppgifter i olika sektioner av fysiken. I uppgifter A: i mekanik - 2-3 i molekylär fysik - 1 i termodynamik - 3 i elektrodynamik - 3-4 i optik - 1-2 i kvantfysik - 1 i atom- och kärnfysik - 1 I uppgifter B: i mekanik - 1 i molekylär fysik - 1 i termodynamik - 1 i elektrodynamik - 1 i optik - 1 i kvantfysik - 1 i atom- och kärnfysik - 1 i uppgifter C: i mekanik - i molekylär fysik - i termodynamik - 1 i elektrodynamik - 1 i optik - 1 i kvantfysik - i atom- och kärnfysik - 1

Vår forskning

A. Analys av fel vid lösning av grafiska problem

Analys av att lösa grafiska problem visade att följande vanliga fel uppstår:

Fel vid läsning av diagram;

Fel i operationer med vektorkvantiteter;

Fel vid analys av isoprocessgrafer;

Fel i det grafiska beroendet av elektriska storheter;

Fel vid konstruktion med hjälp av geometrisk optiks lagar;

Fel i grafiska uppgifter om kvantlagar och den fotoelektriska effekten;

Fel i tillämpningen av atomfysikens lagar.

B. Sociologisk undersökning

För att ta reda på hur skolelever är medvetna om grafiska uppgifter har vi gjort en sociologisk undersökning.

Vi ställde följande frågor till eleverna och lärarna på vår skola: profiler:

1. Vad är en grafisk uppgift?

a) problem med bilder;

b) uppgifter som innehåller diagram, diagram;

c) Jag vet inte.

2. Vad är grafiska uppgifter till för?

b) att utveckla förmågan att bygga grafer;

c) Jag vet inte.

3. Kan du lösa grafiska problem?

a) ja; b) nej; c) inte säker ;

4. Vill du lära dig att lösa grafiska problem?

A) ja ; b) nej; c) Jag har svårt att svara.

50 personer intervjuades. Som ett resultat av undersökningen erhölls följande data:

SLUTSATSER:

Som ett resultat av arbetet med projektet "Graphical Tasks" studerade vi funktionerna i grafiska uppgifter.
Vi studerade funktionerna i metodiken för att lösa grafiska problem.
Vi analyserade typiska fel.
Gjorde en sociologisk undersökning.

Aktivitetsreflektion:

Det var intressant för oss att arbeta med problemet med grafiska uppgifter.
Vi lärde oss hur man forskar, jämför och kontrasterar forskningsresultat.
Vi fann att behärskning av metoder för att lösa grafiska problem är nödvändig för att förstå fysiska fenomen.
Vi fick reda på att behärskning av metoder för att lösa grafiska problem är nödvändig för att lyckas med Unified State Exam.

Om ett linjärt programmeringsproblem bara har två variabler kan det lösas grafiskt.

Betrakta ett linjärt programmeringsproblem med två variabler och:
(1.1) ;
(1.2)
Här finns godtyckliga siffror. Uppgiften kan vara antingen att hitta maximum (max) eller att hitta minimum (min). Systemet med begränsningar kan innehålla både tecken och tecken.

Konstruktion av domänen av genomförbara lösningar

Den grafiska metoden för att lösa problem (1) är som följer.
Först ritar vi koordinataxlarna och väljer skalan. Var och en av olikheterna i systemet av begränsningar (1.2) definierar ett halvplan som begränsas av motsvarande räta linje.

Så, den första ojämlikheten
(1.2.1)
definierar ett halvplan som begränsas av en rät linje. På ena sidan av denna raka linje och på andra sidan. På den mycket raka linjen. För att ta reda på vilken sida ojämlikheten (1.2.1) håller väljer vi en godtycklig punkt som inte ligger på linjen. Därefter ersätter vi koordinaterna för denna punkt med (1.2.1). Om olikheten håller, så innehåller halvplanet den valda punkten. Om ojämlikheten inte håller, så är halvplanet placerat på andra sidan (innehåller inte den valda punkten). Skugga halvplanet för vilket ojämlikheten (1.2.1) gäller.

Vi gör samma sak för de återstående ojämlikheterna i systemet (1.2). På så sätt får vi skuggade halvplan. Punkterna i regionen med genomförbara lösningar tillgodoser alla ojämlikheter (1.2). Därför, grafiskt, är regionen för genomförbara lösningar (ADA) skärningspunkten mellan alla konstruerade halvplan. Skuggning av ODR. Det är en konvex polygon vars ytor tillhör de konstruerade räta linjerna. En ODF kan också vara en obegränsad konvex figur, ett segment, en stråle eller en rak linje.

Det kan också uppstå att halvplanen inte innehåller gemensamma punkter. Då är domänen av genomförbara lösningar den tomma uppsättningen. Det här problemet har inga lösningar.

Metoden kan förenklas. Du behöver inte skugga varje halvplan, utan konstruera först alla raka linjer
(2)
Välj sedan en godtycklig punkt som inte tillhör någon av dessa linjer. Ersätt koordinaterna för denna punkt i systemet med ojämlikheter (1.2). Om alla ojämlikheter är uppfyllda, begränsas området med möjliga lösningar av de konstruerade räta linjerna och inkluderar den valda punkten. Vi skuggar området med möjliga lösningar längs linjernas gränser så att det inkluderar den valda punkten.

Om minst en ojämlikhet inte är uppfylld, välj en annan punkt. Och så vidare tills en punkt hittas vars koordinater uppfyller systemet (1.2).

Att hitta extremumet av den objektiva funktionen

Så vi har en skuggad region av genomförbara lösningar (ADA). Den begränsas av en streckad linje som består av segment och strålar som hör till de konstruerade räta linjerna (2). ODS är alltid en konvex uppsättning. Det kan antingen vara en avgränsad uppsättning eller inte avgränsad längs vissa riktningar.

Nu kan vi leta efter extremumet av den objektiva funktionen
(1.1) .

För att göra detta, välj valfritt nummer och bygg en rak linje
(3) .
För att underlätta ytterligare presentation antar vi att denna raka linje går genom ODR. På denna linje är målfunktionen konstant och lika med . en sådan rät linje kallas en funktionsnivålinje. Denna räta linje delar planet i två halvplan. På ett halvplan
.
På ett annat halvplan
.
Det vill säga, på ena sidan av den räta linjen (3) ökar målfunktionen. Och ju längre vi flyttar punkten från den räta linjen (3), desto större blir värdet. På andra sidan rät linje (3) minskar objektivfunktionen. Och ju längre vi flyttar punkten från rät linje (3) till andra sidan, desto mindre blir värdet. Om vi drar en rät linje parallellt med linje (3), så kommer den nya räta linjen också att vara en nivålinje för målfunktionen, men med ett annat värde.

För att hitta det maximala värdet för objektivfunktionen är det därför nödvändigt att dra en rät linje parallell med den räta linjen (3), så långt som möjligt från den i riktning mot ökande värden, och passera genom minst en punkt av ODD. För att hitta minimivärdet för objektivfunktionen är det nödvändigt att rita en rät linje parallell med den räta linjen (3) och så långt som möjligt från den i riktning mot minskande värden och passera genom minst en punkt av ODD.

Om ODR är obegränsad kan det uppstå ett fall då en sådan direkt linje inte kan dras. Det vill säga, oavsett hur vi tar bort den räta linjen från nivålinjen (3) i riktning mot att öka (minskande), kommer den räta linjen alltid att passera genom ODR. I det här fallet kan den vara godtyckligt stor (liten). Därför finns det inget maxvärde (minimivärde). Problemet har inga lösningar.

Låt oss betrakta fallet när den extrema linjen parallell med en godtycklig linje av formen (3) passerar genom en vertex av ODR-polygonen. Från grafen bestämmer vi koordinaterna för denna vertex. Sedan bestäms det maximala (minsta) värdet för målfunktionen av formeln:
.
Lösningen på problemet är
.

Det kan också finnas ett fall när den räta linjen är parallell med en av ytorna på ODR. Sedan passerar den räta linjen genom två hörn av ODR-polygonen. Vi bestämmer koordinaterna för dessa hörn. För att bestämma det maximala (minsta) värdet för objektivfunktionen kan du använda koordinaterna för någon av dessa hörn:
.
Problemet har oändligt många lösningar. Lösningen är vilken punkt som helst på segmentet mellan punkterna och , inklusive punkterna och sig själva.

Ett exempel på att lösa ett linjärt programmeringsproblem med den grafiska metoden

Uppgiften

Företaget tillverkar klänningar av två modeller A och B. Tre typer av tyg används. För att göra en klänning av modell A krävs 2 m tyg av den första typen, 1 m tyg av den andra typen, 2 m tyg av den tredje typen. För att göra en klänning av modell B krävs 3 m tyg av den första typen, 1 m tyg av den andra typen, 2 m tyg av den tredje typen. Lagren av tyg av den första typen är 21 m, av den andra typen - 10 m, av den tredje typen - 16 m. Frisläppandet av en produkt av typ A ger en inkomst på 400 den. enheter, en produkt typ B - 300 den. enheter

Gör upp en produktionsplan som ger företaget störst inkomst. Lös problemet grafiskt.

Lösning

Låt variablerna och beteckna antalet producerade klänningar, modell A respektive B. Då blir mängden tyg av den första typen som konsumeras:
(m)
Mängden tyg av den andra typen som förbrukas kommer att vara:
(m)
Mängden tyg av den tredje typen som förbrukas kommer att vara:
(m)
Eftersom antalet producerade klänningar inte kan vara negativt, alltså
Och .
Intäkterna från de producerade klänningarna blir:
(den. enheter)

Sedan har den ekonomisk-matematiska modellen av problemet formen:

Vi löser det grafiskt.
Vi ritar koordinataxlarna och .

Vi bygger en rak linje.
Kl.
Kl.
Rita en rak linje genom punkterna (0; 7) och (10.5; 0).

Vi bygger en rak linje.
Kl.
Kl.
Rita en rak linje genom punkterna (0; 10) och (10; 0).

Vi bygger en rak linje.
Kl.
Kl.
Rita en rak linje genom punkterna (0; 8) och (8; 0).

Vi skuggar området så att punkten (2; 2) faller in i den skuggade delen. Vi får fyrhörningen OABC.

(A1.1) .
Kl.
Kl.
Rita en rak linje genom punkterna (0; 4) och (3; 0).

Vi noterar vidare att eftersom koefficienterna för och för den objektiva funktionen är positiva (400 och 300), ökar den allt eftersom och ökar. Vi ritar en rät linje parallell med den räta linjen (A1.1), så långt som möjligt från den i riktning mot ökande , och passerar genom minst en punkt på fyrhörningen OABC. En sådan linje går genom punkt C. Från konstruktionen bestämmer vi dess koordinater.
.

Lösningen på problemet: ;

Svar

.
Det vill säga, för att få den största inkomsten är det nödvändigt att göra 8 klänningar av modell A. Inkomsten blir 3200 den. enheter

Exempel 2

Uppgiften

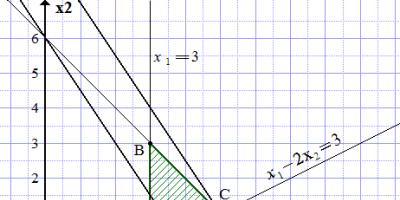
Lös ett linjärt programmeringsproblem grafiskt.

Lösning

Vi löser det grafiskt.
Vi ritar koordinataxlarna och .

Vi bygger en rak linje.
Kl.
Kl.
Rita en rak linje genom punkterna (0; 6) och (6; 0).

Vi bygger en rak linje.
Härifrån.
Kl.
Kl.
Rita en rak linje genom punkterna (3; 0) och (7; 2).

Vi bygger en rak linje.
Vi bygger en rak linje (abskissaxel).

Området för tillåtna lösningar (ADA) begränsas av de konstruerade raka linjerna. För att ta reda på vilken sida märker vi att punkten tillhör ODR, eftersom den uppfyller systemet med ojämlikheter:

Vi skuggar området längs gränserna för de konstruerade linjerna så att punkten (4; 1) faller in i den skuggade delen. Vi får triangel ABC.

Vi bygger en godtycklig linje av nivån på målfunktionen, till exempel,
.
Kl.
Kl.
Rita en rak nivålinje genom punkterna (0; 6) och (4; 0).
Eftersom målfunktionen ökar med ökande och , drar vi en rät linje parallellt med nivålinjen och så långt som möjligt från den i riktning mot ökande , och passerar genom minst en punkt i triangeln ABC. En sådan linje går genom punkt C. Från konstruktionen bestämmer vi dess koordinater.
.

Lösningen på problemet: ;

Svar

Exempel på ingen lösning

Uppgiften

Lös ett linjärt programmeringsproblem grafiskt. Hitta maximi- och minimivärdet för objektivfunktionen.

Lösning

Vi löser problemet grafiskt.
Vi ritar koordinataxlarna och .

Vi bygger en rak linje.
Kl.
Kl.
Rita en rak linje genom punkterna (0; 8) och (2.667; 0).

Vi bygger en rak linje.
Kl.
Kl.
Rita en rak linje genom punkterna (0; 3) och (6; 0).

Vi bygger en rak linje.
Kl.
Kl.
Rita en rät linje genom punkterna (3; 0) och (6; 3).

De räta linjerna är koordinataxlarna.

Området för tillåtna lösningar (ADA) begränsas av de konstruerade räta linjerna och koordinataxlarna. För att ta reda på vilken sida märker vi att punkten tillhör ODR, eftersom den uppfyller systemet med ojämlikheter:

Vi skuggar området så att punkten (3; 3) faller in i den skuggade delen. Vi får ett obegränsat område avgränsat av den streckade linjen ABCDE.

Vi bygger en godtycklig linje av nivån på målfunktionen, till exempel,
(A3.1) .
Kl.
Kl.
Rita en rak linje genom punkterna (0; 7) och (7; 0).
Eftersom koefficienterna för och är positiva, ökar den med ökande och .

För att hitta det maximala måste du rita en parallell linje, som är så långt borta som möjligt i riktning mot ökande , och passerar genom minst en punkt i regionen ABCDE. Men eftersom området är obegränsat på sidan av stora värden på och , kan en sådan rät linje inte dras. Oavsett vilken linje vi drar kommer det alltid att finnas punkter i regionen som ligger längre bort i riktning mot att öka och . Därför finns det inget maximum. du kan göra den så stor som du vill.

Vi letar efter ett minimum. Vi ritar en rät linje parallell med rät linje (A3.1) och så långt som möjligt från den i riktning mot minskande , och passerar genom minst en punkt i regionen ABCDE. En sådan linje går genom punkt C. Från konstruktionen bestämmer vi dess koordinater.
.
Minsta värde för målfunktionen:

Svar

Det finns inget maxvärde.
Minsta värde
.

Ofta gör en grafisk representation av en fysisk process den mer visuell och underlättar därmed förståelsen av fenomenet i fråga. Ibland gör det möjligt att avsevärt förenkla beräkningar, grafer används ofta i praktiken för att lösa olika problem. Förmågan att bygga och läsa dem är obligatoriskt för många specialister idag.

Vi betraktar följande uppgifter som grafiska uppgifter:

för konstruktion, där ritningar och ritningar är till stor hjälp;
scheman lösta med hjälp av vektorer, grafer, diagram, diagram och nomogram.

1) Bollen kastas vertikalt uppåt från marken med en initial hastighet v O. Rita en graf över bollens hastighet kontra tid, förutsatt att stötarna på marken är perfekt elastiska. Försumma luftmotståndet. [lösning]

2) En passagerare som kom för sent till tåget märkte att den näst sista bilen passerade honom ti = 10 s, och den sista - för t2 = 8 s. Förutsatt att tågets rörelse accelereras jämnt, bestäm fördröjningstiden. [lösning]

3) I ett högt rum H en lätt fjäder med styvhet är fäst i taket i ena änden k, med en längd i det odeformerade tillståndet l o (l o< H ). Ett höjdblock placeras på golvet under fjädern x med basyta S, gjord av material med en densitet ρ . Konstruera en graf över blockets tryck på golvet kontra blockets höjd. [lösning]

4) Buggen kryper längs axeln Oxe. Bestäm medelhastigheten för dess rörelse i området mellan punkterna med koordinater x 1 = 1,0 m Och x 2 = 5,0 m, om det är känt att produkten av insektens hastighet och dess koordinat förblir konstant hela tiden, lika med c = 500 cm2/s. [lösning]

5) Till ett massablock 10 kg en kraft appliceras på en horisontell yta. Med tanke på att friktionskoefficienten är lika med 0,7 , definiera:

friktionskraft för fallet om F = 50 N och riktad horisontellt.
friktionskraft för fallet om F = 80 N och riktad horisontellt.
rita en graf över blockets acceleration mot den horisontellt applicerade kraften.
Vilken är den minsta kraft som krävs för att dra i repet för att flytta blocket jämnt? [lösning]

6) Det finns två rör anslutna till blandaren. Varje rör har en kran som kan användas för att reglera vattenflödet genom röret och ändra det från noll till maxvärdet J o = 1 l/s. Vatten rinner i rör vid temperaturer ti = 10°C Och t2 = 50°C. Rita en graf över det maximala flödet av vatten som strömmar ut ur blandaren kontra vattnets temperatur. Försumma värmeförluster. [lösning]

7) Sent på kvällen en ung man lång h går längs kanten på en horisontell rak trottoar med konstant hastighet v. På distans l Det finns en lyktstolpe från kanten av trottoaren. Den brinnande lyktan är fixerad på höjden H från jordens yta. Konstruera en graf över rörelsehastigheten för skuggan av en persons huvud beroende på koordinaten x. [lösning]